problem solving ratio problems

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

In order to access this I need to be confident with:

This topic is relevant for:

Ratio Problem Solving

Here we will learn about ratio problem solving, including how to set up and solve problems. We will also look at real life ratio problems.

There are also ratio problem solving worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is ratio problem solving?

Ratio problem solving is a collection of word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities . They are usually written in the form a:b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are,

• What is the ratio involved?
• What order are the quantities in the ratio?
• What is the total amount / what is the part of the total amount known?
• What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that we can use to help us find an answer. 

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods we can use when given certain pieces of information.

When solving ratio problems it is very important that you are able to use ratios. This includes being able to use ratio notation. 

For example, Charlie and David share some sweets in the ratio of 3:5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

We use the ratio to divide 40 sweets into 8 equal parts. 

Then we multiply each part of the ratio by 5.

3 x 5:5 x 5 = 15:25

This means that Charlie will get 15 sweets and David will get 25 sweets.

• Dividing ratios

Step-by-step guide: Dividing ratios (coming soon)

Ratios and fractions (proportion problems)

We also need to consider problems involving fractions. These are usually proportion questions where we are stating the proportion of the total amount as a fraction.

Simplifying and equivalent ratios

• Simplifying ratios

Equivalent ratios

Units and conversions ratio questions

Units and conversions are usually equivalent ratio problems (see above).

• If £1:\$1.37 and we wanted to convert £10 into dollars, we would multiply both sides of the ratio by 10 to get £10 is equivalent to \$13.70.
• The scale on a map is 1:25,000. I measure 12cm on the map. How far is this in real life, in kilometres? After multiplying both parts of the ratio by 12 you must then convert 12 \times 25000=300000 \ cm to km by dividing the solution by 100 \ 000 to get 3km.

Notice that for all three of these examples, the units are important. For example if we write the mapping example as the ratio 4cm:1km, this means that 4cm on the map is 1km in real life.

Top tip: if you are converting units, always write the units in your ratio.

Usually with ratio problem solving questions, the problems are quite wordy . They can involve missing values , calculating ratios , graphs , equivalent fractions , negative numbers , decimals and percentages .

Highlight the important pieces of information from the question, know what you are trying to find or calculate , and use the steps above to help you start practising how to solve problems involving ratios.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

Explain how to do ratio problem solving

Ratio problem solving worksheet

Get your free ratio problem solving worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on ratio

Ratio problem solving is part of our series of lessons to support revision on ratio . You may find it helpful to start with the main ratio lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• How to work out ratio  
• Ratio to fraction
• Ratio scale
• Ratio to percentage

Ratio problem solving examples

Example 1: part:part ratio.

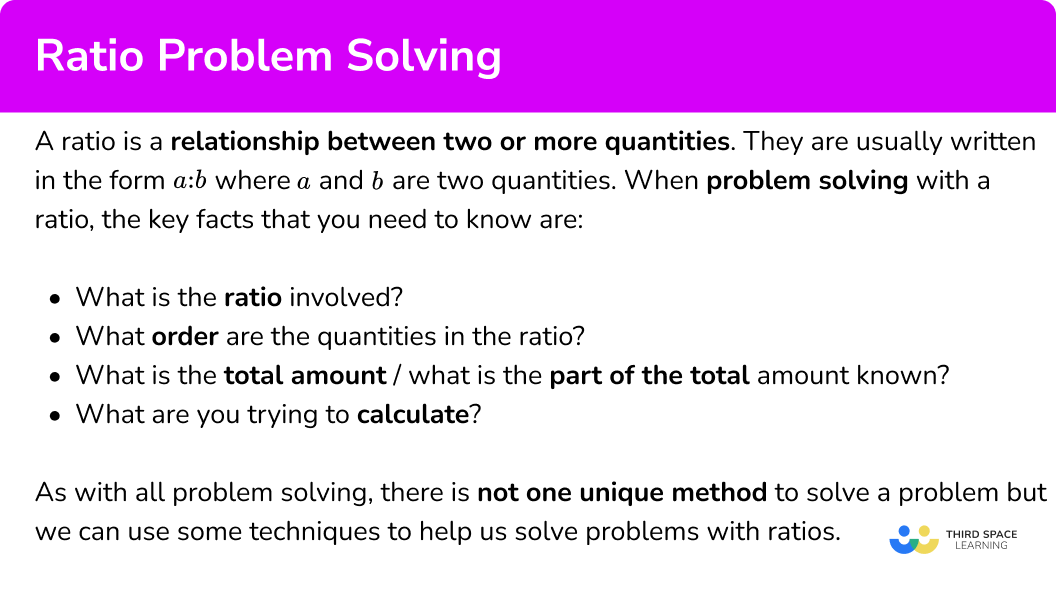
Within a school, the number of students who have school dinners to packed lunches is 5:7. If 465 students have a school dinner, how many students have a packed lunch?

Within a school, the number of students who have school dinners to packed lunches is \bf{5:7.} If \bf{465} students have a school dinner , how many students have a packed lunch ?

Here we can see that the ratio is 5:7 where the first part of the ratio represents school dinners (S) and the second part of the ratio represents packed lunches (P).

We could write this as

Where the letter above each part of the ratio links to the question.

We know that 465 students have school dinner.

2 Know what you are trying to calculate.

From the question, we need to calculate the number of students that have a packed lunch, so we can now write a ratio below the ratio 5:7 that shows that we have 465 students who have school dinners, and p students who have a packed lunch.

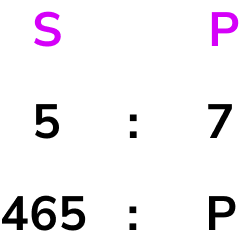
We need to find the value of p.

3 Use prior knowledge to structure a solution.

We are looking for an equivalent ratio to 5:7. So we need to calculate the multiplier. We do this by dividing the known values on the same side of the ratio by each other.

So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

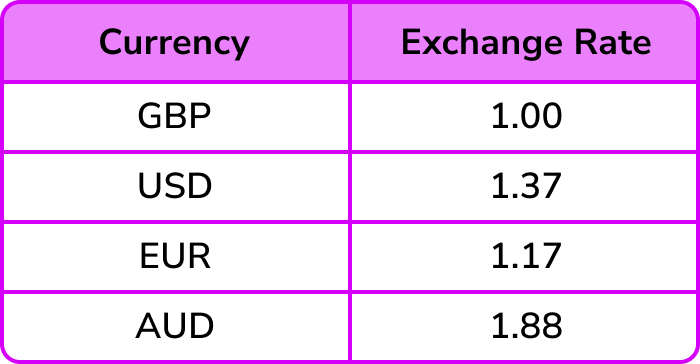
Use the table above to convert £520 (GBP) to Euros € (EUR).

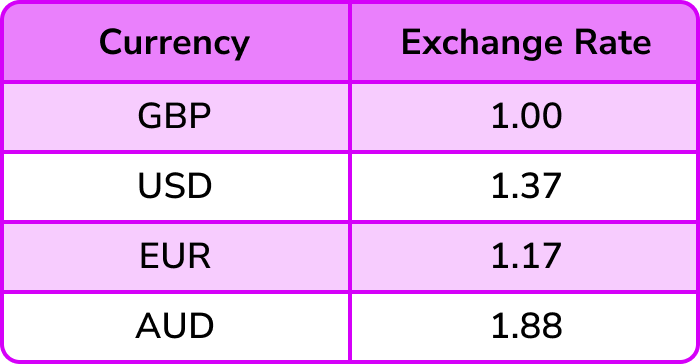
Use the table above to convert \bf{£520} (GBP) to Euros \bf{€} (EUR).

The two values in the table that are important are GBP and EUR. Writing this as a ratio, we can state

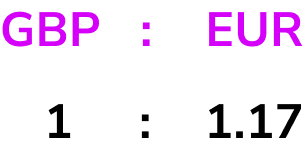
We know that we have £520.

We need to convert GBP to EUR and so we are looking for an equivalent ratio with GBP = £520 and EUR = E.

To get from 1 to 520, we multiply by 520 and so to calculate the number of Euros for £520, we need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520 = €608.40.

Example 3: writing a ratio 1:n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500ml of concentrated plant food must be diluted into 2l of water. Express the ratio of plant food to water respectively in the ratio 1:n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500ml} of concentrated plant food must be diluted into \bf{2l} of water . Express the ratio of plant food to water respectively as a ratio in the form 1:n.

Using the information in the question, we can now state the ratio of plant food to water as 500ml:2l. As we can convert litres into millilitres, we could convert 2l into millilitres by multiplying it by 1000.

2l = 2000ml

So we can also express the ratio as 500:2000 which will help us in later steps.

We want to simplify the ratio 500:2000 into the form 1:n.

We need to find an equivalent ratio where the first part of the ratio is equal to 1. We can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

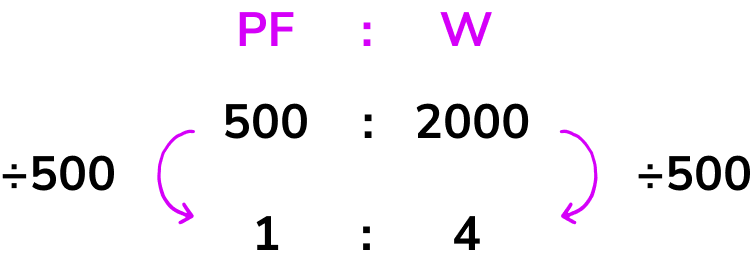
So the ratio of plant food to water in the form 1:n is 1:4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives £8 pocket money, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their ages. Kieran is \bf{3} years older than Josh . Luke is twice Josh’s age. If Luke receives \bf{£8} pocket money, how much money do the three siblings receive in total ?

We can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, we have

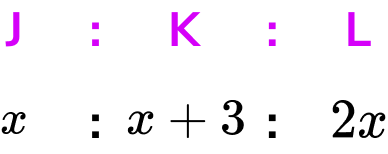
We also know that Luke receives £8.

We want to calculate the total amount of pocket money for the three siblings.

We need to find the value of x first. As Luke receives £8, we can state the equation 2x=8 and so x=4.

Now we know the value of x, we can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

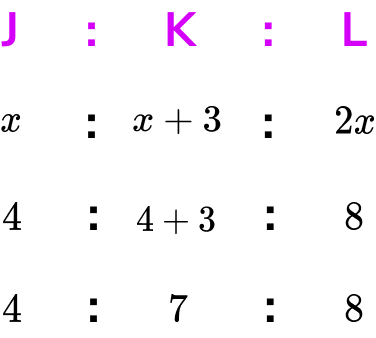
The total amount of pocket money is therefore 4+7+8=£19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colours of counters in a bag.

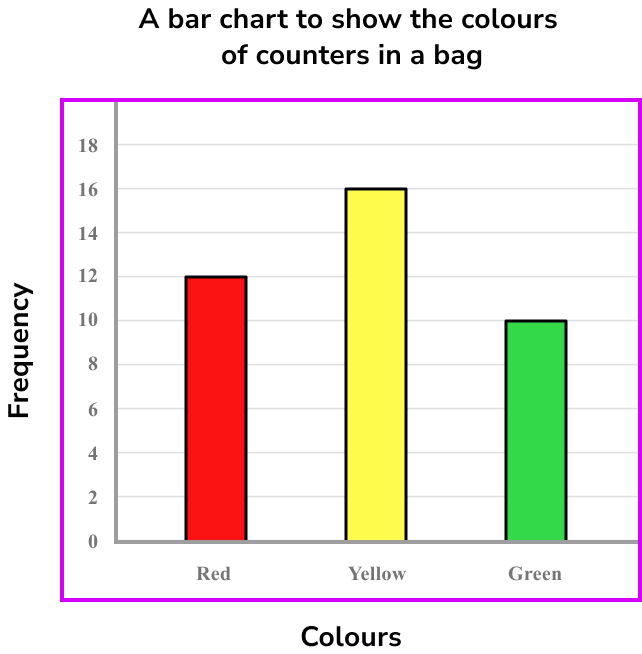
Express this data as a ratio in its simplest form.

From the bar chart, we can read the frequencies to create the ratio.

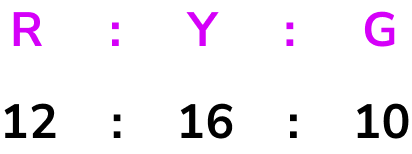
We need to simplify this ratio.

To simplify a ratio, we need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} &12 = 1, {\color{red} 2}, 3, 4, 6, 12 \\\\ &16 = 1, {\color{red} 2}, 4, 8, 16 \\\\ &10 = 1, {\color{red} 2}, 5, 10 \end{aligned}

HCF (12,16,10) = 2

Dividing all the parts of the ratio by 2 , we get

Our solution is 6:8:5 .

Example 6: combining two ratios

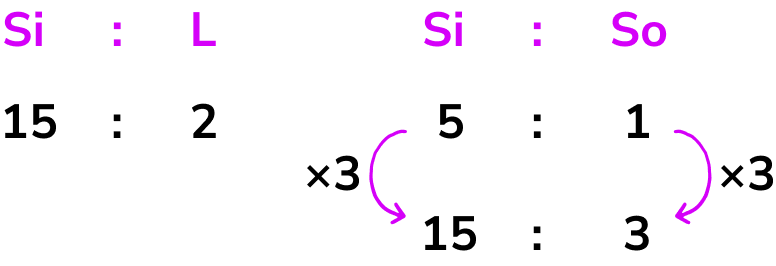
Glass is made from silica, lime and soda. The ratio of silica to lime is 15:2. The ratio of silica to soda is 5:1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15:2.} The ratio of silica to soda is \bf{5:1.} State the ratio of silica:lime:soda .

We know the two ratios

We are trying to find the ratio of all 3 components: silica, lime and soda.

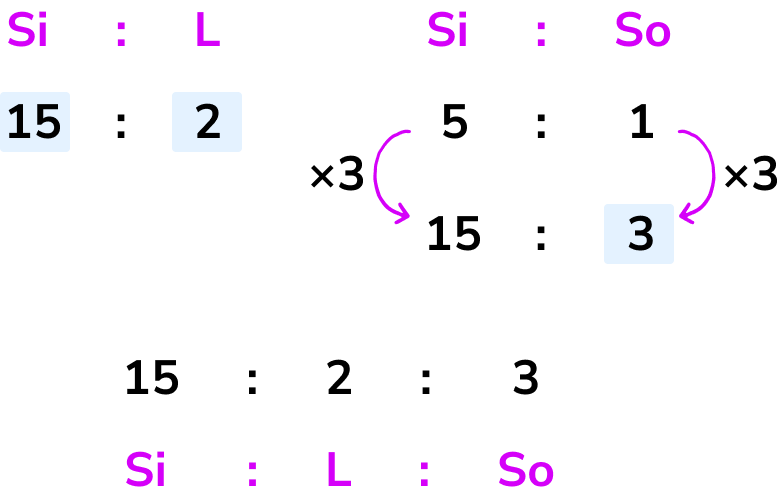
Using equivalent ratios we can say that the ratio of silica:soda is equivalent to 15:3 by multiplying the ratio by 3.

We now have the same amount of silica in both ratios and so we can now combine them to get the ratio 15:2:3.

Example 7: using bar modelling

India and Beau share some popcorn in the ratio of 5:2. If India has 75g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5:2.} If India has \bf{75g} more popcorn than Beau , what was the original quantity?

We know that the initial ratio is 5:2 and that India has three more parts than Beau.

We want to find the original quantity.

Drawing a bar model of this problem, we have

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if we can find out this value, we can then find the total quantity.

From the question, India’s share is 75g more than Beau’s share so we can write this on the bar model.

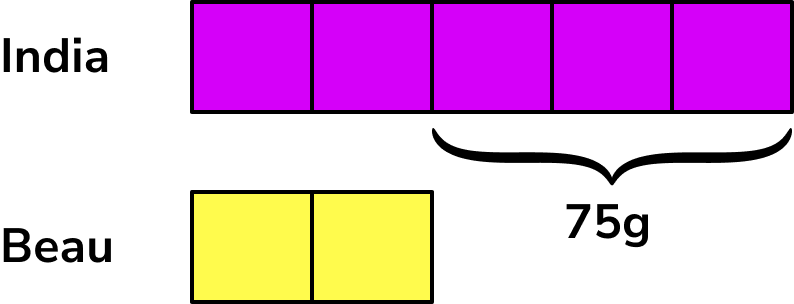
We can find the value of one share by working out 75 \div 3=25g.

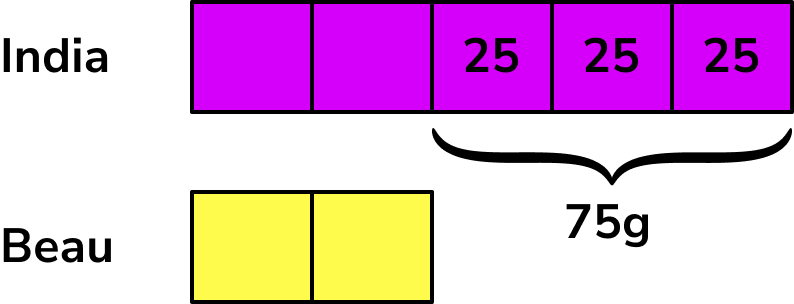
We can fill in each share to be 25g.

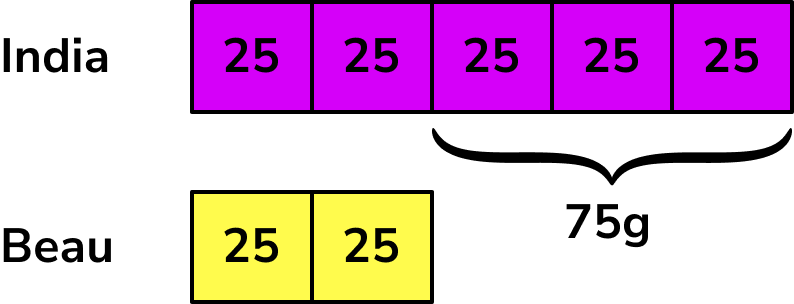
Adding up each share, we get

India = 5 \times 25=125g

Beau = 2 \times 25=50g

The total amount of popcorn was 125+50=175g.

Common misconceptions

• Mixing units

Make sure that all the units in the ratio are the same. For example, in example 6 , all the units in the ratio were in millilitres. We did not mix ml and l in the ratio.

• Ratio written in the wrong order

For example the number of dogs to cats is given as the ratio 12:13 but the solution is written as 13:12.

• Ratios and fractions confusion

Take care when writing ratios as fractions and vice-versa. Most ratios we come across are part:part. The ratio here of red:yellow is 1:2. So the fraction which is red is \frac{1}{3} (not \frac{1}{2} ).

• Counting the number of parts in the ratio, not the total number of shares

For example, the ratio 5:4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.

• Ratios of the form \bf{1:n}

The assumption can be incorrectly made that n must be greater than 1 , but n can be any number, including a decimal.

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3:8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

3. The ratio of prime numbers to non-prime numbers from 1-200 is 45:155. Express this as a ratio in the form 1:n.

4. The angles in a triangle are written as the ratio x:2x:3x. Calculate the size of each angle.

5. A clothing company has a sale on tops, dresses and shoes. \frac{1}{3} of sales were for tops, \frac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

6. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2:3 and the ratio of cloud to rain was 9:11. State the ratio that compares sunshine:cloud:rain for the month.

Ratio problem solving GCSE questions

1. One mole of water weighs 18 grams and contains 6.02 \times 10^{23} water molecules.

Write this in the form 1gram:n where n represents the number of water molecules in standard form.

2. A plank of wood is sawn into three pieces in the ratio 3:2:5. The first piece is 36cm shorter than the third piece.

Calculate the length of the plank of wood.

5-3=2 \ parts = 36cm so 1 \ part = 18cm

3. (a) Jenny is x years old. Sally is 4 years older than Jenny. Kim is twice Jenny’s age. Write their ages in a ratio J:S:K.

(b) Sally is 16 years younger than Kim. Calculate the sum of their ages.

Learning checklist

You have now learned how to:

• Relate the language of ratios and the associated calculations to the arithmetic of fractions and to linear functions
• Develop their mathematical knowledge, in part through solving problems and evaluating the outcomes, including multi-step problems
• Make and use connections between different parts of mathematics to solve problems

The next lessons are

• Compound measures
• Best buy maths

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Algebra: Ratio Word Problems

Related Pages Two-Term Ratio Word Problems More Ratio Word Problems Algebra Lessons

In these lessons, we will learn how to solve ratio word problems that have two-term ratios or three-term ratios.

Ratio problems are word problems that use ratios to relate the different items in the question.

The main things to be aware about for ratio problems are:

• Change the quantities to the same unit if necessary.
• Write the items in the ratio as a fraction .
• Make sure that you have the same items in the numerator and denominator.

Printable Introduction to Ratios

Ratio Word Problems using Tape diagrams Ratio Problems given One of Quantities Ratio Problems given Total Ratio Problems given Difference Ratio Problems with Change of Ratio

Online Ratio of Quantities Ratio Word Problems I Ratio Word Problems II Ratio Word Problems III Ratio Word Problems IV Ratio with Algebra

Ratio Problems: Two-Term Ratios

Example 1: In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there?

Solution: Step 1: Assign variables: Let x = number of red sweets.

Step 2: Solve the equation. Cross Multiply 3 × 120 = 4 × x 360 = 4 x

Answer: There are 90 red sweets.

Example 2: John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane?

Solution: Step 1: Sentence: Jane has 20 marbles, all of them either red or blue. Assign variables: Let x = number of blue marbles for Jane 20 – x = number red marbles for Jane

Step 2: Solve the equation

Cross Multiply 3 × x = 2 × (20 – x ) 3 x = 40 – 2 x

John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane.

Answer: John has 4 more blue marbles than Jane.

How To Solve Word Problems Using Proportions?

This is another word problem that involves ratio or proportion.

Example: A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour. How much sugar should I use?

How To Solve Proportion Word Problems?

When solving proportion word problems remember to have like units in the numerator and denominator of each ratio in the proportion.

• Biologist tagged 900 rabbits in Bryer Lake National Park. At a later date, they found 6 tagged rabbits in a sample of 2000. Estimate the total number of rabbits in Bryer Lake National Park.
• Mel fills his gas tank up with 6 gallons of premium unleaded gas for a cost of $26.58. How much would it costs to fill an 18 gallon tank? 3 If 4 US dollars can be exchanged for 1.75 Euros, how many Euros can be obtained for 144 US dollars?

Ratio problems: Three-term Ratios

Example 1: A special cereal mixture contains rice, wheat and corn in the ratio of 2:3:5. If a bag of the mixture contains 3 pounds of rice, how much corn does it contain?

Solution: Step 1: Assign variables: Let x = amount of corn

Step 2: Solve the equation Cross Multiply 2 × x = 3 × 5 2 x = 15

Answer: The mixture contains 7.5 pounds of corn.

Example 2: Clothing store A sells T-shirts in only three colors: red, blue and green. The colors are in the ratio of 3 to 4 to 5. If the store has 20 blue T-shirts, how many T-shirts does it have altogether?

Solution: Step 1: Assign variables: Let x = number of red shirts and y = number of green shirts

Step 2: Solve the equation Cross Multiply 3 × 20 = x × 4 60 = 4 x x = 15

5 × 20 = y × 4 100 = 4 y y = 25

The total number of shirts would be 15 + 25 + 20 = 60

Answer: There are 60 shirts.

Algebra And Ratios With Three Terms

Let’s study how algebra can help us think about ratios with more than two terms.

Example: There are a total of 42 computers. Each computer runs one of three operating systems: OSX, Windows, Linux. The ratio of the computers running OSX, Windows, Linux is 2:5:7. Find the number of computers that are running each of the operating systems.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled stories
• Sight words
• Sentences & passages
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

Ratio word problems

Download & Print Only $7.90

Use ratios to solve these word problems

Students can use simple ratios to solve these word problems ; the arithmetic is kept simple so as to focus on the understanding of the use of ratios.

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

Simplifying Ratios Pixel Picture ( Editable Word | PDF | Answers ​ )

Simplifying Ratios Odd One Out ( Editable Word | PDF | Answers )

Equivalent Ratios Match-Up ( Editable Word | PDF | Answers ​ )

Working with Ratio Practice Strips ( Editable Word | PDF | Answers )

Dividing in a Ratio Practice Strips ( Editable Word | PDF | Answers )

Dividing in a Ratio Fill in the Blanks ( Editable Word | PDF | Answers )

Dividing in a Ratio Crack the Code ( Editable Word | PDF | Answers )

Combining Ratios Practice Strips ( Editable Word | PDF | Answers )

Sharing and Combining Ratios Practice Strips ( Editable Word | PDF | Answers )

Solving Ratio Problems Practice Strips ( Editable Word | PDF | Answers )

Solving Ratio Problems Practice Grid ( Editable Word | PDF | Answers )

Harder Ratio Problems Practice Strips ( Editable Word | PDF | Answers )

Fractions and Ratio Worded Problems Practice Strips ( Editable Word | PDF | Answers )

Unitary Method Practice Strips ( Editable Word | PDF | Answers )

Unitary Method Match-Up ( Editable Word | PDF | Answers )

Best Buys Practice Strips ( Editable Word | PDF | Answers )

Best Buys Fill in the Blanks ( Editable Word | PDF | Answers )

Currency Conversions Practice Strips ( Editable Word | PDF | Answers )

Proportion Worded Problems Practice Strips ( Editable Word | PDF | Answers )

Proportion Worded Problems Practice Grid ( Editable Word | PDF | Answers )

Mixed Ratio and Proportion Revision Practice Grid ( Editable Word | PDF | Answers ​ )

Ratio and Proportion Word Problems — Examples & Practice - Expii

Ratio and proportion word problems — examples & practice, explanations (4).

Ratio and Proportion Word Problems

Ratio and proportion word problems are really applicable to real life when you need to calculate costs, determine time limits, or even convert between measurement systems ! Here's a breakdown of what a ratio and proportion word problem might look like. We'll also see how to understand what the problem is asking, and how to solve it!

Image by Caroline Kulczycky

It's important to note that in Step Two, when you plug the appropriate values into the proportion, the units in both the numerators must be the same, and the units in both the denominators must be the same. For example, in the graphic above, the units in the numerators are books. The units in the denominators are hours. If the units given to you in the word problem are not consistent, you must somehow make them match. This next problem will show you how. For certain units we will use conversion factors to help make the units the same. We don't always have conversion factors, but it's good to know what ones we do have. Here are some examples:

• Units of length: convert between feet and meters
• Units of mass: convert between grams and kilograms
• Units of time: convert between minutes and days

Once that's done, the numerators will have the same units as each other. Likewise for the denominators. Then we'll be able to solve the proportion just using algebra. The equation will have a variable times a number on one side, and a number on the other side. Thus we can solve the equation in one step using division .

Practice Problem

Trisha can make 5 pairs of earrings in 1 week. Assuming she works at this constant rate, how many complete pairs of earrings can she make in 10 days?

Related Lessons

Math in Music: Rhythm

Now that the basic concepts of ratios and proportions have been covered, we are going to dive a little deeper into working with them through the subject of music.

Ratios are found in music within two main concepts: Rhythm/Polyrhythm and Pitch Intervals . These may seem a little foreign right now, but I promise they won't be too hard to understand. This explanation will focus on Rhythm and Polyrhythm, but the explanation on Pitch Intervals has been linked above.

Rhythm/Polyrhythm

All rhythms are referred to by names based off of fractions/ratios. There are whole notes (44 of a measure), half notes (24 of a measure), quarter notes (14 of a measure), eighth notes (18 of a measure), sixteenth notes (116 of a measure), etc. and the name denotes how much of a 4 beat measure the note takes up, as shown below. For our purposes, we are always going to use a 4 beat measure to describe our ratios.

In order, Whole Note, Half Note, Quarter Note, Eighth Note, Sixteenth Note, all taking up the same amount of time

Not all notes and rhythms are based on groups of 4, notes can be based on any division! Triplets can be used to split a four beat measure into groups of 3 or 6 instead of groups of 2 or 4.

Three half note triplets take up a measure, 6 quarter note triplets, 12 eighth note triplets, etc.

The brackets over the notes tell how many notes are played in the span of the bracket. You can see the 3 placed above all of the notes. This is because each group of 3 takes a set amount of time. The half note triplets take up 4 beats (one full measure) with 3 notes, the quarter note triplets take up 2 beats (one half of a measure) with 3 notes, and the eighth note triplets take up 1 beat (one quarter of a measure) with 3 notes. As ratios, these could be written as 3:4, 3:2, and 3:1. If we wanted to write these notes as fractions, they could be called 13, 16, and 112 notes.

When we start combining these rhythms to be played at the same time, we get what are called polyrhythms. These are normally defined by ratio of how many notes are being played in the same amount of time.

The ratios in this case are going to be written in terms of the top line against the bottom line. The first measure is a 4:3 while the second measure is a 3:2. These same polyrhythms can be written without needing a second line to compare by once again using the brackets above the notes.

The groupings on the top line both take up an entire measure, 4 beats. That means that the first measure on the top line shows a 5:4 ratio (aka five-lets), and the second shows a 7:4 (aka seven-lets) ratio. The bottom groupings take up 2 beats , so they show a 5:2 and 7:2 ratio.

We're gonna try a practice question that builds on some of these concepts.

Brandon is playing a trombone solo that has 24 evenly spaced notes. How many evenly spaced notes would Libby need to play in her counter melody to make the entire section a 4:3 polyryhthm?

(Video) Proportion Examples and Word Problems

by Math Meeting

This video by Math Meeting explains proportions and works through a few examples.

A proportion is two ratios that are set equal to one another.

An example of a proportion would be: 1 dollar10 pesos=10 dollars100 pesos As you can see, they are equivalent. The units are the same, and then we notice the fractions are equivalent . The fractions are equivalent because 10100 can be reduced to 110.

If you multiply the numerator and denominator of the first ratio by 10, you get the second ratio. If you have 10 times more dollars, you will have 10 times more pesos.

The standard proportion problem is as follows: 5x=103 You are given two proportions and you want to solve for x.

The best way to solve these types of equations is with cross multiplication .

To cross multiply, you take the product of the numerator of the first ratio and the denominator of the second ratio. Set that equal to the product of the numerator of the second ratio and the denominator of the first ratio.

Let's solve this problem now. 5x=103⇒5⋅3=x⋅1015=10x1510=10x10315210=10x1032=x

Another Example

Here's a word problem using proportions.

The currency in Spain is the euro. If I exchange $250 at the airport, how many euros will I get in return? (1 euro = 1.38 dollars)

The parentheses at the bottom give us our first ratio. 1 euro1.38 dollars

Within the question itself is our second ratio. x euros250 dollars

Set them equal to each other. Remember that the same units have to be in the top/bottom. 11.38=x250

To solve, we cross multiply. 11.38=x250⇒1⋅250=1.38⋅x250=1.38x2501.38=1.38x1.382501.38=1.38x1.38181.16=x

You will get approximately 181.16 euros!

Math in Music: Pitch

Ratios are found in music within two main concepts: Rhythm/Polyrhythm and Pitch Intervals . These may seem a little foreign right now, but I promise they won't be too hard to understand. This explanation is going to cover Pitch and Intervals, and Rhythm/Polyrhythm is linked above.

Pitch and Intervals

When two notes are being played at once, there is an Interval between the two pitches . Every pitch can be written as both a note (think A,B,C, and their placings on a staff) or as a measurement of Hertz (Hz). We are going to use A=440 Hz as a baseline to demonstrate how ratios are used in intervals and tuning in music.

As notes move in octaves, there is always a 2:1 ratio between the notes. Based on A at 440 Hz, the A one octave higher is going to be measured at 880 Hz, and the A one octave lower is going to be measured at 220 Hz.

This pattern continues in both directions (up and down) from A in the second space until eventually the note is outside of the range of human hearing.

The ratios between notes exist for every interval and are the basis for tuning many instruments as well as playing in tune with another musician. For example, were going to use the next two most common intervals, the perfect fifth and the major third. Using A=440 Hz as a basis again, we are going to use the intervals of 3:2 to find the measurement of the perfect fifth (E), and a ratio of 5:4 to find the major third (C# or C Sharp).

In this case we are going to put 440 as a denominator because we want to find the Hz of a note that is higher than our original A.

32=x4402x=1320x=660

Our perfect fifth of E will be at 660 Hz when it is perfectly in tune. Now lets calculate the pitch of the major third, C#. Once again, the 440 is going to be in the denominator as we are finding a note higher than A.

54=x4404x=2220x=550

Our major third of C# is going to be at 550 Hz when perfectly in tune. Combining all of these notes, you get a nice consonant A major chord. Just to make sure our musical brains are keeping up with the math, here is what this looks like on a staff.

Let's try a practice problem to see if everything is sticking.

Brandon and Libby are trying to practice their duet. If Brandon is playing a low A at 220 Hz, and Libby wants to play a perfectly in tune F# that is one octave and a major sixth (5:3) higher, what pitch should she play?

366.67 Hz

733.33 Hz

440 Hz

550 Hz