mobile edge computing research papers

Help | Advanced Search

Computer Science > Distributed, Parallel, and Cluster Computing

Title: mobile edge computing.

Abstract: Mobile Edge Computing (MEC) has emerged as a solution to the high latency and suboptimal Quality of Experience (QoE) associated with Mobile Cloud Computing (MCC). By processing data near the source, MEC reduces the need to send information to distant data centers, resulting in faster response times and lower latency. This paper explores the differences between MEC and traditional cloud computing, emphasizing architecture, data flow, and resource allocation. Key technologies like Network Function Virtualization (NFV) and Software-Defined Networking (SDN) are discussed for their role in achieving scalability and flexibility. Additionally, security and privacy challenges are addressed, underscoring the need for robust frameworks. We conclude with an examination of various edge computing applications and suggest future research directions to enhance the effectiveness and adoption of MEC in the evolving technological landscape.

Submission history

Access paper:.

• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

A Comprehensive Survey on Mobile Edge Computing: Challenges, Tools, Applications

Ieee account.

• Change Username/Password
• Update Address

Purchase Details

• Payment Options
• Order History
• View Purchased Documents

Profile Information

• Communications Preferences
• Profession and Education
• Technical Interests
• US & Canada: +1 800 678 4333
• Worldwide: +1 732 981 0060
• Contact & Support
• About IEEE Xplore
• Accessibility
• Terms of Use
• Nondiscrimination Policy
• Privacy & Opting Out of Cookies

A not-for-profit organization, IEEE is the world's largest technical professional organization dedicated to advancing technology for the benefit of humanity. © Copyright 2024 IEEE - All rights reserved. Use of this web site signifies your agreement to the terms and conditions.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 02 December 2024

An edge server placement based on graph clustering in mobile edge computing

• Shanshan Zhang 1 ,
• Jiong Yu 1 &
• Mingjian Hu 2  

Scientific Reports volume  14 , Article number:  29986 ( 2024 ) Cite this article

623 Accesses

Metrics details

• Computer science
• Information technology

With the exponential growth of mobile devices and data traffic, mobile edge computing has become a promising technology, and the placement of edge servers plays a key role in providing efficient and low-latency services. In this paper, we investigate the issue of edge server placement and user allocation to reduce transmission delay between base stations and servers, and balance the workload of individual servers. To this end, we propose a graph clustering-based edge server placement model by fully considering the constraints such as the distance, coverage area and number of channels of base stations. The model mainly consists of a two-layer graph convolutional network (GCN) component and a differentiable version of K -means clustering component, which transforms the server placement problem into an end-to-end learning optimization problem on a graph. It trains the GCN network to achieve the best clustering results with the expectation of average delay and load balancing as the loss function to obtain the edge server placement and user assignment scheme. We conducted experiments based on the Shanghai Telecom dataset, and the results show the effectiveness of our approach in both latency reduction and load balancing.

Similar content being viewed by others

Research on collaborative edge network service migration strategy based on crowd clustering

Graph neural network-based cell switching for energy optimization in ultra-dense heterogeneous networks

QOGMP: QoS-oriented global multi-path traffic scheduling algorithm in software defined network

Introduction.

The convergence of wireless communication innovation and the resurgence of artificial intelligence has propelled the evolution of the mobile communication system from facilitating “human connection” to enabling “thing connection”. Currently, the system is advancing towards the realm of “smart connection of everything”. In tandem with this transformation, the number of mobile devices and data traffic is experiencing exponential growth. As projected by the International Data Corporation (IDC), the year 2025 will witness a staggering 80 billion internet-connected devices and a mobile data traffic volume of 160 ZB, equivalent to an astounding 16 trillion GB. Confronted with such colossal amounts of data, conventional cloud computing technology falls short in meeting the stringent communication latency requirements of specific applications, including AR/VR and Telematics 1 . Addressing this challenge, mobile edge computing (MEC) facilitates the migration of computing, storage, network and application services from centralized data centers to the network edge 2 , 3 . This deployment model, involving servers or small-scale data centers on edge devices, ensures low latency, high bandwidth and reliable service support, thereby catering to the diverse application demands of mobile users.

In the context of mobile edge computing, the performance, energy consumption, and user experience of the entire system are directly influenced by the placement of edge servers 4 . Hence, studying the placement strategy of these servers is critical to achieving efficient mobile edge computing. However, the task of edge server placement extends beyond simply selecting server locations; it also involves the allocation of compute resources to users. An effective deployment plan should take into account multiple factors: Firstly, it should strive to minimize latency for user devices, thereby enhancing the quality of service across various applications, especially in latency-sensitive scenarios; Secondly, load balancing of edge servers must be considered, as an excessive number of idle servers would lead to unnecessary energy waste; Furthermore, placing more servers in densely populated areas helps avoid server overload, which can result in failures 5 . For actual AR/VR applications, the low latency and load balancing brought about by the reasonable placement of edge servers can ensure that a large number of customers can enjoy a high-quality user experience even during peak hours, which strengthens user stickiness and thus increases the enterprise’s economic returns. For Vehicle Networking, such as autonomous driving scenarios, low latency can ensure that vehicles receive and process key information such as road conditions and traffic signals in a timely manner, allowing the decision-making system to react quickly; load balancing can ensure that edge servers will not be delayed due to processing too much data when there is heavy traffic flow, guaranteeing the stable operation of the entire transportation system and vehicle safety. For edge server providers, providing low latency improves customer satisfaction and increases financial returns, while load balancing avoids maintenance costs due to overloads leading to failures and wasted energy due to idle servers. Numerous research findings have emerged to address the issue of edge server placement. Some studies have utilized mathematical models and algorithms to optimize server placement, improving system performance and energy efficiency 6 , 7 , 8 , 9 . Additionally, other studies have explored determining server placement based on distinct application scenarios and user requirements 10 , 11 , 12 , 13 , 14 . These research provides invaluable support and guidance for the practical implementation of mobile edge computing.

However, the edge server placement problem is essentially a complex network optimization problem, which involves multiple nodes (e.g., users, base stations, edge servers, etc.) and the connectivity relationships among them (e.g., data transmission links, communication delays, etc.). These nodes and connectivity relationships constitute a typical graph structure. GCN 15 , as a neural network specifically designed to process graph data, is able to efficiently capture and utilize the complex information in this graph structure. Through multi-layer convolutional operations, GCN is able to progressively extract deeper features of nodes, thus more accurately reflecting their positions and roles in the network. User assignment, as an integral part of the edge server placement problem, can be viewed as clustering in the graph, and K-means, as an unsupervised learning algorithm, has the advantages of low computational complexity, good stability and repeatability. In the edge server placement problem, the combined application of GCN and K-means can fully utilize their respective advantages. Based on this, we propose a graph clustering-based edge server placement method called GCESP. first, GCN is used to extract deep feature representations of the nodes in the graph data (a graph consisting of base stations); then, nodes are clustered based on these feature representations using a microscopic K-means clustering algorithm; then, back-propagation is performed using average delay and load balancing as loss functions. The GCN parameters are adjusted to obtain better feature representations to achieve better clustering results; finally, the placement of edge servers and user allocation scheme are determined based on the clustering results.

Overall, the main contributions of our work are as follows:

We investigate the edge server placement problem in MEC and introduce the utilization of GCN for the first time to address this issue. In order to fully utilize the distance relationship between base stations, we convert the base station location data into a directed weighted graph. The weights of the edges are related to the coverage and number of channels of the base stations and the distance between two base stations.

We formulate the edge server placement problem as an end-to-end learning optimization problem in graphs and propose a graph clustering-based edge server placement strategy called GCESP. This algorithm trains the GCN to generate the embedded representation of base stations with minimizing the average delay and load balancing as the loss function, which enables the differentiable K -means components to obtain clusters with high objective values. The cluster center is the location where the edge servers are placed, and users are assigned to the nearest edge server.

We conducted convergence experiments on the GCESP algorithm and experimentally selected the learning rate, performance weights and number of algorithm iterations suitable for the edge server placement problem in this paper. The learning rate of the The effectiveness of the proposed algorithm in terms of average latency and load balancing metrics as well as scalability is verified by conducting multiple sets of comparison experiments on the Shanghai Telecom dataset.

The remainder of this paper is organized as follows: section “ Related works ” presents an extensive overview of the existing work on the edge server placement problem, discussing the achievements and limitations of previous research efforts. Section “ System model and problem description ” establishes a system model for the edge server placement problem and the problem definitions and performance metrics are introduced to establish a clear framework for analysis and evaluation. In section “ Graph Clustering-based edge server placement ”, we introduce a graph clustering-based strategy for edge server placement. Section “ Experiments and results ” details the experimental study conducted to evaluate the performance of the four compared approaches. Lastly, section “ Conclusion ” concludes this paper by summarizing the key findings and offering insights into potential directions for future research.

Related works

With the advancement of MEC technologies, the placement problem of edge servers has garnered increasing attention. Previous studies have approached the edge server placement problem from four key perspectives: (1) Latency minimization 16 : This objective aims to optimize network performance by minimizing the latency between users and services. Various distance metrics are utilized to approximate latency. In this case, edge servers should be placed at the nearest points to users. (2) Deployment cost minimization 17 , 18 , 19 , 20 while limiting maximum latency: The goal here is to reduce network operational costs, minimize the number of servers, and enhance operational efficiency. Edge servers should be placed with the minimum number required to meet network performance requirements. (3) Latency and deployment cost tradeoff optimization 5 , 21 : This objective aims to strike a balance that minimizes the number of servers and operational costs while fulfilling network performance requirements. (4) Maximizing user connectivity within the cluster 22 , i.e., coverage: This goal focuses on maximizing network service coverage to meet the needs of a greater number of users and improve service accessibility. Edge servers should be placed in locations that can cover the maximum number of users.

These studies consider multiple sets of placement function parameters, such as the number of servers, geographic location, individual server capacity, and server location priority. Consequently, they employ different layout methods: (1) Graph theory-based algorithms: Zeng et al. 17 transformed the edge server placement problem into a minimum dominating set problem in graph theory. They proposed greedy algorithms based on different edge server capacity conditions and simulated annealing-based algorithms to find solutions that minimize the number of edge servers while meeting latency requirements. (2) Clustering-based algorithms: Jia et al. 16 introduced a density-based clustering (DBC) algorithm to optimize cloudlet locations and user-to-cloudlet assignments in dynamic wireless metropolitan area networks (WMAN), thereby reducing average task waiting time. They also proposed a K -median algorithm to address cloudlet placement in WMAN scenarios. Mohan et al. 18 devised the Anveshak framework, which employs distance and density-based clustering algorithms to determine optimal edge server locations, considering both deployment and operational costs while meeting user requirements. (3) Linear programming-based algorithms: Bouet et al. 23 formulated the edge server placement problem as a mixed integer linear programming and proposed a graph-based algorithm that partitions MEC clusters to consolidate communication at the edge while considering maximum MEC server capacity. Xu et al. 21 cast the capacity small cloud placement problem as an integer linear programming (ILP), offering an efficient heuristic and an online algorithm to handle dynamic user request allocation. Yao et al. 24 considered heterogeneous cloudlet servers with varying costs and resource capacities. They formulated the cloudlet placement problem as integer linear programming and developed a low-complexity heuristic algorithm. (4) Mixed-integer programming-based algorithms: Mondal et al. 19 introduced the CCOMPASSION framework, formulating a nonlinear mixed-integer procedure to determine the optimal Cloudlet placement location that minimizes installation costs while satisfying capacity and latency constraints. Guo et al. 25 proposed an approximate method using K -means and mixed-integer quadratic programming approximation to solve the edge cloud placement problem in MEC environments, reducing mobile user service communication delays while ensuring server load balancing. (5) Multi-objective optimization-based algorithms: Wang et al. 26 formulated the edge server placement problem in a smart city mobile edge computing environment as a multi-objective constrained optimization problem. They utilized mixed-integer programming to identify optimal solutions for reducing access latency between mobile users and edge servers and balancing edge server workload. Bhatta et al. 20 transformed the heterogeneous cloudlet placement problem into a multi-objective integer programming model and proposed a genetic algorithm-based approach to reduce deployment costs while guaranteeing latency requirements. (6) Hierarchical tree-based algorithms: This category of algorithms employs a tree structure to represent the relationship between users and servers. Server placement is determined using hierarchical tree structure algorithms 27 , 28 . (7) Heuristic-based algorithms: Ma et al. 29 presented a new heuristic algorithm (NHA) and a particle swarm optimization algorithm (PSO) for addressing delay problems caused by WMAN. The particle swarm optimization algorithm, known for its simplicity and fast convergence, is a population-based optimization method that making it more suitable than NHA for larger scale cloudlet placement problems. Li et al. 5 designed a particle swarm optimization-based algorithm to optimize profit and introduced a weight factor q to guarantee transmission delay and correct base station assignment. Additionally, a service level agreement is utilized to strike a balance between transmission delay and energy consumption trade-offs. Recently, many applications based on heuristic algorithms or their improved algorithms for the edge server placement problem have appeared 30 , 31 , 32 , 33 , 34 , and such algorithms are usually suitable for the edge server placement problem because they have better flexibility and can adapt to different sizes and types of networks. However, they also suffer from the problems of over-dependence on parameters and easy to fall into local optimums, while the improved algorithms, although solving the above problems to a certain extent, also increase the computational complexity and the performance is not stable enough.

Graph neural networks have demonstrated powerful capabilities in processing graph data 35 . Researchers have successfully applied them in various domains, such as speech field, computer vision field, and natural language processing field, etc 36 , 37 , 38 , 39 , 40 . In terms of placement, Weidong Zhang et al. 41 based on the graph convolutional network (GCN) algorithm, which combines node features and graph structure features, they proposed a new method for optimal sensor location applicable to the conditions of irregular network systems. Zhuo Chen et al. 42 Considering the cost of various resources occupied for service provision as revenue and service efficiency and energy consumption as cost, a mixed integer programming (MIP) model is developed to describe the optimal deployment of container clusters (CC) on edge service nodes. In addition, a Deep Reinforcement Learning (DRL) and Graph Convolutional Network (GCN) framework (RL-GCN) based on behavioral critique is proposed to solve the optimization problem. The framework can obtain the optimal placement strategy through self-learning based on the requirements and objectives of CC placement. In particular, by introducing GCN, the features of correlation relationship among multiple containers in CC can be effectively extracted to improve the placement quality. Some studies have applied graph neural networks to edge computing scenarios, but few studies have used them directly to solve the placement problem of edge servers. Chen Ling et al. 43 believe that predicting the resource requirements of users has a significant impact on the placement of edge servers. They use the PSO algorithm to solve the edge server placement problem by using a graph convolutional network-based network traffic model to generate the network traffic distribution. WeiWei Miao et al. 44 assume that neighbouring edge servers have similar resource load patterns. They use a graph neural network to capture the connections between servers, which is then linked to an LSTM layer to produce predictions of server workloads.

Wilder et al. 45 developed the CLUSTERNET system, which combines graph link prediction learning and graph optimization problems. The first component of this algorithm structure is trained based on the objectives of the downstream optimization task, which involves fine-tuning the embedding representation to generate clusters with high objective values. However, this system is a general framework for solving graph partitioning (e.g., community detection, maxcut, etc.) and subset selection (e.g., facility location, impact maximization, immunization, etc.), primarily focusing on minimizing the maximum distance in the facility location problem. In this paper, we aim to find an improved solution to the edge server placement problem by conducting an in-depth analysis of the relationship between each base station node in the mobile edge computing system.

Model diagram of the edge server placement system in a mobile edge computing scenario.

System model and problem description

In this section, we establish the system model of the edge server placement problem in a MEC environment, provide the problem definition for edge server placement and introduces two crucial performance metrics: average latency and load balancing. Table 1 shows some key symbols and their descriptions.

System model

In the MEC environment, the edge server placement system can be considered as a network with a stable topology. This network consists of a cloud data center, edge servers deployed at base stations, cellular base stations, and a variety of terminal devices. Figure 1 illustrates a system model featuring three edge servers. This system can be represented as an undirected graph denoted as \(G=\left( V,E \right)\) , where \(V=B\cup S\) denotes the set of nodes in graph G . Here, \(B=\left\{ b_{1},b_{2}\dots ,b_{n} \right\}\) denotes the set of the base stations; \(S=\left\{ s_{1}, s_{2}\dots ,s_{m} \right\}\) denotes the set of the edge servers; and \(E=\left\{ e_{ij}|i\in n,j\in m \right\}\) represents the set of edges in graph G , which signifies the connections between the base stations. The relationship between the base station and the server is inherently included, given that the server is placed at the location of the base station. In a cellular mobile network, the signal coverage of each base station is denoted by \(d_{max}\) , which represents the coverage radius. Furthermore, the spherical distance between any two base stations denoted as \(\rho \left( b_{i},b_{j} \right)\) , can be computed using Haversine’s formula as in Eq. ( 1 ). For \(\rho \left( b_{i},b_{j} \right) \le d_{max}\) , \(e_{ij}\) is assigned the value of 1, otherwise , \(e_{ij}\) is set to 0.

where R denotes the radius of the earth in Km and r epresents the radian value, specifically \(\frac{\pi }{180 }\) . The longitude and latitude of base station \(b_{i}\) are denoted as \(lat_{i}\) , \(lng_{i}\) , while \(lat_{j}\) , \(lng_{j}\) represent the longitude and latitude of base station \(b_{j}\) , respectively.

Service requests sent by mobile users within the coverage range of a base station are collected by the base station and forwarded to the edge server for processing. This can occur either directly or through other base stations within range. Taking the example of \(s_{2}\) in Fig. 1 , the edge server \(s_{2}\) is located at base station \(b_{2}\) , enabling direct processing of service requests collected by base stations \(b_{1}\) , \(b_{3}\) , and \(b_{4}\) within the signal coverage of \(b_{2}\) . However, base station \(b_{5}\) is located outside the coverage range of \(b_{2}\) and must forward its request data to the server through the intermediate base station \(b_{4}\) . It is important to note that the network topology may have multiple connection paths between nodes, but this paper considers the default usage of the shortest path.

Problem description

In MEC scenario, the edge server placement problem can be defined as follows: A set of base stations, denoted as \(B=\left\{ b_{1},b_{2},\dots , b_{n}\right\}\) , along with a set of edge servers , denoted as \(S=\left\{ s_{1}, s_{2}\dots ,s_{m} \right\}\) , are provided for the edge server placement problem. The objective is to select m base stations from the given n stations as the locations to deploy the edge servers, and subsequently assign the base stations to these edge servers. The placement scheme of edge servers is denoted by \(\alpha ^{s} =\left\{ \alpha _{s_{k},b_{j}}|s_{k} \in S, b_{j}\in B \right\}\) , where \(\alpha _{s_{k},b_{j}}= 1\) when server \(s_{k}\) is placed at base station \(b_{j}\) , and 0 otherwise. Similarly, the assignment scheme of base stations is denoted by \(\alpha ^{b} =\left\{ \alpha _{b_{i},s_{k}}|b_{i}, \in B ,s_{k} \in S \right\}\) , where \(\alpha _{b_{i},s_{k}}\) = 1 when base station \(b_{i}\) is assigned to the edge server \(s_{k}\) , and 0 otherwise. Note that the edge server placement problem studied in this paper concerns only the initial deployment of edge servers. Once deployed, the location of the edge servers generally does not change, and later expansion can be done by upgrading the hardware configurations of the edge servers such as compute and storage capacity, or by directly adding additional edge servers.

Transmission delay

The edge server placement scheme mainly affects the backhaul delay from the base station to the server. Therefore, this study focuses on the backhaul delay (referred to as transmission delay in this paper). Specifically, the transmission delay between a base station and the base stations in its coverage area can be directly measured based on the straight-line distance between them. Whereas for transmission delay between it and other base stations outside its coverage area, the shortest path needs to be calculated. The transmission delay between any two base stations, denoted as \(d\left( b_{i},b_{j}\right)\) , is determined using Eq. ( 2 ), where \(floyd\left( b_{i},b_{j}\right)\) represents the shortest path between the two base stations.

The average transmission delay of all base stations to their assigned edge servers in the system can be calculated by Eq. ( 3 ).

Load balancing

Load balancing, which can prevent server overload or underutilization, is a crucial metric for evaluating the edge server placement policy. In this paper, it is assumed that all edge servers have the same computational power and are configured to satisfy all the amount of computational tasks received. By achieving load balancing, we can ensure that users of each server experience similar computational and queuing latencies.

Load balancing can be quantified by examining the variance of the workload, which is defined as:

where \(w_{s_{k}}\) representes the workload of server \(s_{k}\) , which corresponds to the cumulative load of the base stations assigned to that server. In turn, the load of base station \(b_{i}\) is denoted as \(w_{b_{i}}\) , and its calculation is outlined in Eq. ( 5 ). Additionally, \(\overline{w_{s}}\) denotes the average workload across all servers, and its determination is provided by Eq. ( 6 ).

Problem definition

Lower average system transmission delay can significantly improve user experience and save communication costs by reducing the amount of data transmitted over the network. Load balancing can improve system scalability and elasticity, and as system load increases, it can automatically adjust resource allocation to ensure that each server is able to process requests efficiently, avoiding system performance degradation due to overloading of certain servers. Therefore, both the average system latency and the load balancing of the edge servers need to be taken into account when placing the edge servers. We model the problem of the placement of edge servers as a multi-objective optimisation problem, which can be formulated as follows:

where \(\mu\) is used to adjust the weights of the two sub-objectives and its value depends on the relative importance of the sub-objectives in the optimization problem. \(Da_{max}\) represents the maximum communication delay in the entire system, while \(Bw_{max}\) denotes the maximum load balancing value, indicating a scenario where all the loads are offloaded to a single edge server. Eqs. ( 10 ) and ( 11 ) outline the calculations for \(Da_{max}\) and \(Bw_{max}\) . \(\sum _{j=0}^{n} \alpha _{s_{k} ,b_{j}}=1\) describes the constraints on edge server placement, i.e., each edge server can only be placed at one base station, while \(\sum _{k=0}^{m} \alpha _{b_{i},s_{k}}=1\) describes the constraints on user assignment, i.e., each base station can only be assigned to one edge server.

Graph clustering-based edge server placement

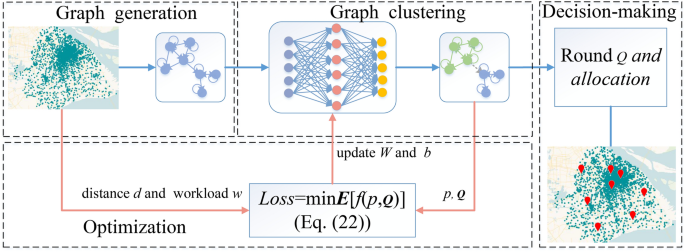
The overall architecture of GCESP (the map was created by the author using the ketoper.gl 3.0.0, https://kepler.gl/demo and the dataset available at http://sguangwang.com/TelecomDataset.html ).

The edge server placement scheme involves addressing two problems: the determination of server locations and the assignment of base stations. To tackle this, we propose an end-to-end learning and optimization approach called graph clustering-based edge server placement (GCESP), which frames the problem as a subset selection and clustering problem in graphs. The overall architecture of the GCESP algorithm is illustrated in Fig. 2 . The GCESP algorithm consists of three modules: (1) Graph generation: The process of converting a base station dataset into a graph is called graph generation which generates a directed weighted graph. (2) Graph clustering and optimization: This module employs a two-layer GCN to process the base station graph data and derive the embedding representation of the base stations. Subsequently, the embedding representation is clustered using differentiable K -means, yielding the probability vector \(\mathscr {Q}=\left\{ q_{1},q_{2}...q_{n}\right\}\) for server placement and the probability matrix \(P=\left\{ p_{jk}|j\in n,k \in m\right\}\) for base station assignment. The GCN is then trained with the objective of minimizing average delay and achieving load balancing, serving as the loss function to optimize the clustering results. (3) Edge server placement and base station assignment: The graph clustering layer provides the probability vector \(\mathscr {Q}\) for placing an edge server at each base station. To obtain the final edge server placement scheme, a fast pipage rounding calculation of \(\mathscr {Q}\) is executed, and subsequently, the base station is assigned to the nearest server.

The remainder of this section, we provide a detailed description of the three modules.

Graph generation

In section “ System model and problem description ” it was mentioned that the mobile edge system exhibits a stable network topology, which can be regarded as an undirected graph. To effectively capture the spatial relationship among the base stations, this paper utilizes the distance between them to determine the edge weights in the graph. In practical scenarios, each base station is constrained by the number of available channels. Therefore, we define the set of neighboring base stations within the coverage area of a given base station j , denoted as \(N \left( b_{j}\right)\) . Specifically, we consider the \(link_{max}\) closest base stations as the neighbors. Consequently, the edge weights can be represented as:

when \(b_{i} \notin \varvec{N}\left( b_{j}\right)\) , the edge weight between \(b_{i}\) and \(b_{j}\) is set to 0. On the contrary, as the distance between them decreases, the edge weight increases. In other words, if base station \(b_{j}\) is selected for placing an edge server, the probability of assigning nearby base stations to this server becomes higher. Since base station \(b_{j}\) is guaranteed to be assigned to this server, the diagonal entry of the adjacency matrix is set to 1. It should be noted that \(w \left( b_{i},b_{j}\right)\) is not necessarily equal to \(w \left( b_{j},b_{i}\right)\) , resulting in a directed graph representation after the graph generation module, which can be expressed using the adjacency matrix \(\mathscr {A}\) . The graph generation process is outlined in Algorithm 1, where line 1 calculates the spherical distances between all base stations using Eq. ( 1 ), lines 2 to 7 calculate the weights of the edges between base stations based on the distances between them, and line 8 sets the diagonal of the adjacency matrix to 1.

Graph Generation

Graph clustering and optimization

The graph clustering module consists of two key components: a graph embedding layer, utilizing the GCN, and a differentiable K -means layer. Initially, the adjacency matrix \({\mathscr{A}}\) derived from the graph generation module and the feature matrix represented by the unit matrix I are fed into the graph embedding layer. This layer, comprising two GCN layers, generates embedded representations for each node in the graph. Subsequently, the K-means algorithm operates within the embedding space to solve the graph clustering problem. By leveraging this algorithm, a soft assignment of node clustering and the corresponding probabilities of each node being the cluster center are obtained. Lastly, the GCN network weights are updated by minimizing the average system delay and achieving load balancing, which serves as the loss function, thus enabling the attainment of optimal clustering outcomes.

Algorithm 2 demonstrates the graphical clustering and optimization process, where line 3 calculates the embedding of the base station nodes, lines 4 to 14 cluster the base stations in the embedding space using the K-means algorithm to obtain the cluster centers and the probability of the base station assignments, lines 15 to 18 arrive at the probability vectors for the base station as the center of the cluster based on the probability of the base station assignments, and lines 19 and 20 combine the latency and load-balancing joint metrics as a loss function to update the parameters of GCN using gradient descent method. The remainder of this section describes the components of this model in detail.

Graph Clustering and Optimization

Network structure of GCN

In the graph embedding layer, a two-layer GCN is employed to facilitate the forward propagation process. The GCN operates as follows:

where \(\mathscr {A}\) is the adjacency matrix obtained from the graph generation module, which primarily contains the location information of the base stations. X represents the input feature matrix, which, in this case, is set as the unit matrix I since the edge server placement strategy focuses on the base station’s location information. The network weights \(w^{(0)} \in R^{D_{1} \times H}\) and biases \(b^{(0)} \in R^{H}\) correspond to the connection between the input layer and the hidden layer. Similarly, the network weights \(w^{(1)} \in R^{H \times D_{2}}\) and biases \(b^{(1)} \in R^{D_{2}}\) represent the connection between the hidden layer and the output layer. Here, \(D_{1}\) denotes the input data dimension, H represents the number of cells in the hidden layer, and \(D_{2}\) refers to the data dimension of the embedding representation.

The inputs to the GCN are the adjacency matrix X and the unit matrix I , and the output is the embedding matrix \(\mathscr {Z}\) with the same adjacency matrix. The structure of GCN is shown in Fig. 3

The network structure of GCN.

K -means clustering

The  K -means clustering is commonly used in edge server placement problems with efficient computational performance. In addition, the clustering component embedded in GCN must be differentiable and k-means is easier to implement.The embedding of node j is represented as \(z_{j}\) , while \(u_{k}\) represents the center of cluster k in the embedding space. Additionally, \(p_{jk}\) denotes the probability that node j belongs to cluster k .

where \(\beta\) is a hyperparameter that, when approaching infinity, restores the standard K -means assignment. While \(\left\| \bullet \right\|\) can be any norm, we use the negative cosine similarity due to its strong empirical performance. By adopting this approach, we transform the binary variable in traditional K -means into a fractional value, allowing for the condition \(\sum _{k=1}^{m} p_{jk}=1\) to hold for all nodes j .

Similar to traditional K -means, a series of iterations can be performed until convergence is achieved, resulting in the output of the forward pass ( u ,  p ). Moreover, the probability of base station j serving as a cluster center (for placing edge servers) can be obtained as follows:

Loss function

In our study, the primary objective of edge server placement is to minimize communication delay and achieve load balancing. Therefore, these two metrics are utilized as loss functions during the training process of GCN to optimize the network parameters.

The probability of placing an edge server at each base station is obtained through graph clustering. As a result, the probability of placing an edge server at base station \(b_{j}\) and assigning base station \(b_{i}\) to the server is determined as follows:

Hence, the average delay of the entire system can be expressed as follows:

The probability \(p_{jk}\) is obtained from the graph clustering process, indicating the assignment probability of each base station to edge server \(s_{k}\) . With this information, we can express the workload of edge server \(s_{k}\) as follows:

Hence, the load balancing of the whole system can be expressed as:

The loss function can be defined as follows based on the derivation above:

Edge server placement and base station assignment

Fast Pipage Rounding Implementation

After performing graph clustering, a continuous solution vector \(\mathscr {Q}\) is obtained, where each \(q_{j}\) (with \(0<q_{j}<1\) ) represents the probability of including base station \(b_{j}\) in the solution. The constraint \(\sum _{j=1}^{n}q_{j}=m\) ensures that the solution contains exactly m base stations. It is important to note that performing a separate rounding calculation for each value in the vector \(\mathscr {Q}\) may result in a vector with more than m values of 1. To address this, we employ a general rounding method known as fast pipage rounding, which is a deterministic procedure for rounding linear relaxations.

Algorithm 3 illustrates the steps involved in this rounding process, line 3 to 4 compares the two elements of the list in turn, and if both values are equal to 0, no value is assigned, line 5 to 14 if the sum of the two values is less than 1, then there is a high probability that the element with the larger value will be assigned the sum of the two values, and the element with the smaller value will be assigned 0, and line 15 to 24 if the sum of the two values is greater than 1, then there is a high probability that the element with the larger value will be assigned 1, and the element with the smaller value will be assigned the sum of the two values minus 1. Upon completing the rounding calculation, we obtain a vector comprising only 0s and 1s, where the base stations associated with a value of 1 indicate the locations where the edge servers are placed. Finally, the edge server placement ends with assigning the base station to the closest edge server. The algorithm is somewhat randomized, so we run it several times to take the best result as the final solution to the edge server placement problem.

Experiments and results

This section presents an overview of the experimental environment and the dataset employed. , and investigates the impact of learning rate, metric weights and number of iterations on the performance of the algorithm. In addition, a comparative analysis is conducted to evaluate the proposed algorithm against six recently proposed server placement algorithms.

Experimental environment and dataset

The experimental environment utilized in this study is based on PyTorch 1.13.0, Python 3.8, and NumPy 1.19.0. For this pilot study, a real-world telecommunications dataset was chosen 5 , 25 , 46 , which comprises 3233 base station locations in Shanghai, represented by latitude and longitude coordinates. It also includes records of Internet access through these base stations over a six-month period, totaling over 7.2 million records. Each node in the accompanying Fig. 4 corresponds to a base station in Shanghai. The dataset captures information such as base station location, date, start time, end time and the mobile phone ID of users accessing the Internet.

In order to illustrate the workload distribution, Table 2 is presented, displaying information on 12 randomly selected base stations from the dataset. Workloads are calculated based on the start and end times of mobile users accessing the Internet. It is evident from the table that the workloads of these base stations exhibit significant imbalance. Hence, when considering the placement of edge servers, load balancing emerges as a critical concern, alongside communication delay.

Distribution of 3233 base stations in Shanghai (the map was created by the author using the ketoper.gl 3.0.0, https://kepler.gl/demo and the dataset available at http://sguangwang.com/TelecomDataset.html ).

Parameter analysis

Learning rate.

The learning rate is an essential hyperparameter in deep learning, which has a significant impact on the training speed of the network and determines the convergence of the loss function. A small learning rate may result in slow convergence or convergence to a local minimum, while a large learning rate can cause oscillation of the loss function beyond the optimal point, leading to failure in convergence. In order to find the learning rate suitable for the edge service placement algorithm, we conducted two sets of experiments, one with the same number of edge servers and the other with the same number of base stations. The Fig. 5 illustrates the effect of learning rate on the convergence results for different combinations of number of base stations and edge servers, the n denotes the number of base stations and the m denotes the number of servers. It can be clearly seen that the GCESP algorithm with a learning rate of 0.0001 exhibits a more stable downward trend and higher performance in solving the edge server placement problem.

Convergence of the GCESP algorithm with different learning rates.

Value of \(\mu\)

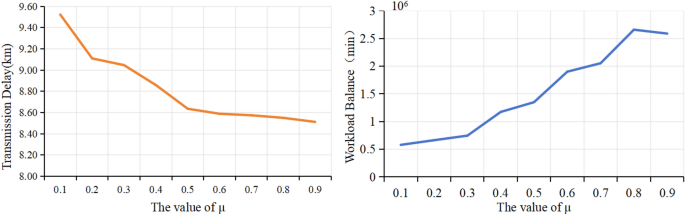
Transmission delay and workload balance with respact to the value of \(\mu\) .

In the problem definition we mention the weight parameter \(\mu\) of the sub-objective, which can adjust the importance of the sub-objective in the optimization problem. To verify this, we make \(\mu\) vary from 0.1 to 0.9 and observe the algorithm performance as shown in Fig. 6 ( \(n=400,m=5\) ). As the weight parameter \(\mu\) escalates, the significance of transmission delay within the optimization objective intensifies, leading to a gradual decline in its value. Notably, this decline becomes more gradual once \(\mu > 0.5\) . Conversely, as \(\mu\) increases, the importance of load balancing in the optimization objective diminishes and exhibits a relatively uniform upward trend.In addition, we can observe that when \(\mu\) changes from 0.6 to 0.7, the change curves of both performance metrics are relatively flat,which may indicate that the algorithm has reached a relatively stable state, so we set \(\mu\) to 0.6 in the later experiments.

Iteration number

In the context of graph optimization algorithms, the number of iterations is often used to control how well the algorithm optimizes the graph structure or the graph data. Through multiple iterations, the algorithm can gradually adjust parameters such as nodes, edges, or weights of the graph to optimize a specific objective function. If the number of iterations is set too low, the algorithm may not converge sufficiently to the optimal solution. This means that the structure or parameters of the graph may not have been tuned optimally, resulting in poor performance of the algorithm. While too many iterations may ensure that the algorithm converges sufficiently, it may also lead to overfitting or waste of computational resources. As depicted in Fig. 7 , it is evident that when the iteration count is below 1000, neither of the performance indicators achieve convergence. Conversely, as the iteration count surpasses 1000, the transmission delay exhibits minimal variation, while the load balancing metric paradoxically demonstrates a tendency to increase. Therefore, we consider that for the edge server placement problem in this paper, 1000 is the best choice for the number of iterations.

Performance comparison

We compare GCESP with other algorithms for the edge server placement problem, e.g., GA 30 , pso 31 , ABC 32 , WOA 33 , nPSO 34 . These are recently emerged heuristic algorithms or their improved versions for applications with the edge server placement problem. Note that the transmission delay is positively correlated with the transmission distance, so in this paper we use the transmission distance (in km) to denote the transmission delay; moreover, the load balance is the standard deviation of the workload (in min).

To enhance the verification of the GCESP algorithm’s performance, We set up three sets of experiments: Firstly, we keep the base station data fixed and vary the number of edge servers; Secondly, we keep the number of edge servers constant and vary the number of base stations; Finally, we expand the number of base stations to 1800 and set the placement rate of edge servers to 0.05. The specific parameter configurations utilized in these experiments can be found in Table 3 .

Results of the comparison experiments

Performance with varying the number of edge servers.

Figure 8 shows the comparison of the seven algorithms in terms of average transmission delay and load balance when the number of base stations is fixed at 400 and the number of edge servers ranges from 5 to 30. It is clear from the figure that as the number of edge servers increases, the average delay and load balance of all the algorithms show a decreasing trend. This is because an increase in the number of edge servers means that more servers are available to share the tasks of the base station, and the base station has more and better options when it needs to offload tasks to the edge servers. The average transmission delay of our proposed algorithm GCESP is almost optimal; the load balancing is inferior to some of the compared algorithms only when the number of edge servers is 10 and 25.

Comparison results with respect to the number of Edge Servers.

Table 4 allows us to quantitatively analyze the results of this set of experiments. When the number of edge servers varies from 5 to 30, for the average transmission delay metric, our proposed algorithm GCESP is 0.19% higher than the nPSO algorithm only when the number of edge servers is 5, and 4.66% lower than the nPSO algorithm on average for the other quantities, and 2.99%, 4.04%, 4.67%, 5.45%, and 3.61% lower than the other comparative algorithms on average, respectively. In terms of load balancing metrics, our proposed algorithm GCESP is on average 12.77% and 17.93% lower than GA and PSOGA; it is 0.14% higher than PSO when the number of edge servers is 5 but 11.07% for other quantities; it is on average 4.36% higher than the ABC algorithm when the number of edge servers is 10 and 25 but on average 8.08%; 9.81% higher than the WOA algorithm when the number of edge servers is 10, but 14.25% lower on average for other quantities; 3.46% higher than the nPSO algorithm when the number of edge servers is 25, but 13.55% lower on average for other quantities.

Comparison results with respect to the number of Base Stations.

Running time comparison results for Experiment 1 and Experiment 2.

Comparative results from Experiment 3 (number of base stations is 1800 and edge server placement percentage is 0.05).

Performance with varying the number of base stations

Figure 9 illustrates the comparative results of the seven algorithms in terms of average latency and load balancing as the number of base stations varies from 200 to 700 while maintaining a fixed count of 10 edge servers. It is evident that as the number of base stations increases, all five algorithms exhibit an upward trend in both average latency and load balancing. The reason for this result is that the increase in the number of base stations means that each edge server has to take on more tasks that are not evenly spread across the base stations, and the base stations do not have many edge servers to choose from when they need to offload tasks. For average transmission delay, our proposed algorithm GCESP is higher than some of the compared algorithms only when the number of base stations is 200 and 300, and lower than the compared algorithms for all other quantities. For load balancing, our proposed algorithm is significantly higher than some of the compared algorithms only when the number of base stations is 400 and 600, and almost reaches the minimum for all other quantities.

Table 5 allows us to quantitatively analyze the results of this set of experiments. When the number of base stations is varied from 200 to 700, for the average transmission delay metric, our proposed algorithm GCESP is on average 1.46% higher than the PSOGA algorithm when the number of base stations is 200 and 300, but 2.60% lower on average for other quantities; 3.32% higher than the nPSO algorithm only when the number of base stations is 200 , but 2.4% lower on average for other quantities; and 2.87%, 2.01%,2.90%, and 3.74% lower than the other comparative algorithms on average. In terms of load balancing metrics, our proposed algorithm GCESP is on average 10.91% and 14.47% lower than GA and PSO; it is on average 6.70% higher than the ABC algorithm when the number of base stations is 400 and 600 but 12.50% lower on average for other quantities;7.87% higher on average than the WOA algorithm when the number of base stations is 200 and 400 but 8.79% lower on average for other quantities;1.31% higher than PSOGA algorithm when the number of base stations is 600 but 19.00% for other quantities; 1.93% higher than the nPSO algorithm when the number of base stations is 700, but 11.51% lower on average for other quantities.

Runtime comparison results

The left panel of Fig. 10 shows the running time of each algorithm in the first set of experiments, and it can be seen that with the increase of the number of edge servers, the running time of the six comparison algorithms all show a more obvious upward trend, the reason is that the more the number of edge servers implies a larger solution space. On the other hand, the running time of our proposed algorithm GCESP does not change much, and after the number of edge servers is larger than 15, its running time is significantly less than that of the six compared algorithms.

The right side of Fig. 10 shows the running time of each algorithm in the second set of experiments, and it can be seen that the running time of the six compared algorithms shows a more obvious upward trend with the increase of the number of base stations, again due to the fact that the higher number of base stations implies a larger solution space. The running time of our proposed algorithm GCESP increases slowly and is in the middle of all the algorithms. It is only slightly higher than PSO and WOA when the number of base stations is 700.

From the results of the runtime comparison between the above two sets of experiments, the computational complexity of the GCESP algorithm is mainly related to the number of base stations, i.e., the size of the graph, and when the number of base stations is fixed, the change of the number of edge servers does not have much impact on the running time. As for the heuristic algorithm as a comparison algorithm, the increase in the number of edge servers represents the increase in the population dimension, the computational complexity increases accordingly, and the running time almost shows a linear increase. When the number of base stations increases i.e., the size of the graph increases, although the running time of the GCESP algorithm increases, the growth trend is relatively flat. The heuristic algorithm, on the other hand, as the number of base stations increases, the search space is enlarged and the convergence speed is gradually reduced, resulting in a substantial increase in the running time. It is important to note, however, that for the edge server placement problem studied in this paper, runtime is not an important performance metric because we focus only on the initial placement of the edge servers and do not address later scaling or dynamic tuning. Therefore, a certain amount of computational overhead is acceptable in order to obtain a more optimal placement strategy.

Performance with larger number of base stations

To further validate the scalability of the GCESP algorithm, we designed a third set of experiments in which the number of base stations is 1800 and the edge server placement rate is 0.05 (i.e., m = 90) . Figure 11 shows the comparison results of the average transmission delay, load balancing and runtime of the seven algorithms under this set of experimental settings. From the figure, it can be seen that the proposed algorithm GCESP is only 3.42% higher than the WOA algorithm in terms of average transmission delay performance, but 5.80% lower than the other five algorithms on average; for load balancing, GCESP is only 0.33% higher than the nPSO algorithm, but 4.12% lower than the other five algorithms on average; and the running time of GCESP is on average 60.21% lower than that of the comparison algorithms.

From the above comparison results, it can be seen that when the number of base stations is expanding, the impact on the performance and convergence speed of the heuristic algorithm is more significant, while the algorithm GCESP proposed in this paper shows a very obvious advantage by guaranteeing the optimization performance while the running time is significantly lower than that of the comparison algorithms. This is due to the fact that in the graph construction process of the algorithm, the coverage range \(d_{max}\) and the maximum number of links \(link_{max}\) of each base station are taken into account, which simplifies the graph to a large extent, thus effectively suppressing the computational overhead brought about by the increase in the size of the graph.

After the above three sets of experiments, we can verify the effectiveness and stability of the algorithm GCESP proposed in this paper in the two performance indexes of transmission delay and load balancing. We attribute this to the fact that the GCESP algorithm combines the graph structure information capturing ability of GCNs with the simplicity and efficiency of k-means clustering to induce clustering with high objective values with downstream tasks (minimizing average latency and load balancing).

This paper presents a transformation of the edge server placement problem into a graph-based clustering optimization problem. The approach involves several steps. Firstly, the base station location data is converted into a directed weighted graph representation, utilizing the distance, the coverage area and number of channels of the base stations. Subsequently, the expectation value function, encompassing average delay and load balancing, is employed as the loss function for graph clustering and optimization. This process aims to obtain the optimal probability vector for placing the edge servers at the base stations. Finally, a fast rounding calculation is employed to derive the final placement policy, with the remaining base stations assigned to the nearest edge servers. To evaluate the performance of the GCESP algorithm, we use the Shanghai Telecom dataset. We have chosen the appropriate learning rate, target weights and number of iterations of the algorithm by iterative experimental validation. Comparative analysis with the optimization algorithm for recent edge server placement shows that GCESP exhibits better results in terms of both average delay and load balancing, and is scalable.

This study provides a new solution to the edge server placement problem, but the combined use of GCN and k-means increases the complexity of hyper-parameter tuning, and how to cope with the challenges of parameter optimization is a worthwhile issue for future research.In addition, this study focuses only on the initial deployment of edge servers, does not address subsequent scaling issues, and considers only basic metrics. Future research efforts will delve into more comprehensive metrics optimization, including deployment cost, energy cost, vendor profitability, and mobile user benefits. In addition, given the mobility of users, it becomes impractical to rely only on a single edge server for service delivery. Therefore, our future work will prioritize dynamic deployment and service migration.

Data availability

The datasets generated and/or analyzed during the current study are available in ( http://sguangwang.com/TelecomDataset.html ).

Hou, J., Chen, M., Geng, H., Li, R. & Lu, J. GP-NFSP: Decentralized task offloading for mobile edge computing with independent reinforcement learning. Future Gener. Comput. Syst. (2023).

Zhao, Y., Li, B., Wang, J., Jiang, D. & Li, D. Integrating deep reinforcement learning with pointer networks for service request scheduling in edge computing. Knowl.-Based Syst. 258 , 109983 (2022).

Article   Google Scholar  

Wang, G., Li, C., Huang, Y., Wang, X. & Luo, Y. Smart contract-based caching and data transaction optimization in mobile edge computing. Knowl.-Based Syst. 252 , 109344 (2022).

Li, Y. & Wang, S. An energy-aware edge server placement algorithm in mobile edge computing. In 2018 IEEE International Conference on Edge Computing (EDGE) , 66–73 (IEEE, San Francisco, CA, 2018).

Li, Y., Zhou, A., Ma, X. & Wang, S. Profit-aware edge server placement. IEEE Internet Things J. 9 , 55–67 (2022).

da Silva, R. A. C. & da Fonseca, N. L. S. On the location of fog nodes in fog-cloud infrastructures. Sensors 19 , 2445 (2019).

Article   ADS   Google Scholar  

Chen, L., Wu, J., Zhou, G. & Ma, L. QUICK: QoS-guaranteed efficient cloudlet placement in wireless metropolitan area networks. J. Supercomput. 74 , 4037–4059 (2018).

Leyva-Pupo, I., Santoyo-González, A. & Cervelló-Pastor, C. A framework for the joint placement of edge service infrastructure and user plane functions for 5G. Sensors 19 , 3975 (2019).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Xu, Z., Liang, W., Xu, W., Jia, M. & Guo, S. Efficient algorithms for capacitated cloudlet placements. IEEE Trans. Parallel Distrib. Syst. 27 , 2866–2880 (2016).

Lu, J., Jiang, J., Balasubramanian, V., Khosravi, M. R. & Xu, X. Deep reinforcement learning-based multi-objective edge server placement in Internet of Vehicles. Comput. Commun. 187 , 172–180 (2022).

Sinky, H., Khalfi, B., Hamdaoui, B. & Rayes, A. Adaptive edge-centric cloud content placement for responsive smart cities. IEEE Netw. 33 , 177–183 (2019).

Xu, L., Ge, M. & Wu, W. Edge server deployment scheme of blockchain in IoVs. IEEE Trans. Reliab. 71 , 500–509 (2022).

Zhang, J. et al. Quantified edge server placement with quantum encoding in internet of vehicles. IEEE Trans. Intell. Transp. Syst. 23 , 9370–9379 (2022).

Zhao, X., Zeng, Y., Ding, H., Li, B. & Yang, Z. Optimize the placement of edge server between workload balancing and system delay in smart city. Peer-to-Peer Netw. Appl. 14 , 3778–3792 (2021).

Du, X., Yu, J., Chu, Z., Jin, L. & Chen, J. Graph autoencoder-based unsupervised outlier detection. Inf. Sci. 608 , 532–550 (2022).

Jia, M., Cao, J. & Liang, W. Optimal cloudlet placement and user to cloudlet allocation in wireless metropolitan area networks. IEEE Trans. Cloud Comput. 5 , 725–737 (2017).

Zeng, F., Ren, Y., Deng, X. & Li, W. Cost-effective edge server placement in wireless metropolitan area networks. Sensors 19 , 32 (2018).

Mohan, N., Zavodovski, A., Zhou, P. & Kangasharju, J. Anveshak: Placing edge servers in the wild. In Proceedings of the 2018 Workshop on Mobile Edge Communications , 7–12 (ACM, Budapest Hungary, 2018).

Mondal, S., Das, G. & Wong, E. CCOMPASSION: A hybrid cloudlet placement framework over passive optical access networks. In IEEE INFOCOM 2018 - IEEE Conference on Computer Communications , 216–224 (2018).

Bhatta, D. & Mashayekhy, L. Generalized cost-aware cloudlet placement for vehicular edge computing systems. In 2019 IEEE International Conference on Cloud Computing Technology and Science (CloudCom) , 159–166 (2019).

Bouet, M. & Conan, V. Mobile edge computing resources optimization: A geo-clustering approach. IEEE Trans. Netw. Serv. Manage. 15 , 787–796 (2018).

Yao, H., Bai, C., Xiong, M., Zeng, D. & Fu, Z. Heterogeneous cloudlet deployment and user-cloudlet association toward cost effective fog computing. Concurr. Comput.: Pract. Exp. 29 , e3975 (2017).

Guo, Y. et al. User allocation-aware edge cloud placement in mobile edge computing. Softw.: Pract. Exp. 50 , 489–502 (2020).

Google Scholar  

Wang, S., Zhao, Y., Xu, J., Yuan, J. & Hsu, C.-H. Edge server placement in mobile edge computing. J. Parallel Distrib. Comput. 127 , 160–168 (2019).

Jiao, J., Chen, L., Hong, X. & Shi, J. A heuristic algorithm for optimal facility placement in mobile edge networks. KSII Transact. Internet Inf. Syst. (TIIS) 11 , 3329–3350 (2017).

Ma, L., Wu, J., Chen, L. & Liu, Z. Fast algorithms for capacitated cloudlet placements. In 2017 IEEE 21st International Conference on Computer Supported Cooperative Work in Design (CSCWD) , 439–444 (2017).

Kasi, S. K. et al. Heuristic edge server placement in industrial internet of things and cellular networks. IEEE Int. Things J. 8 , 10308–10317 (2020).

Pandey, C., Tiwari, V., Pattanaik, S. & Sinha Roy, D. A strategic metaheuristic edge server placement scheme for energy saving in smart city. In 2023 International Conference on Artificial Intelligence and Smart Communication (AISC) , 288–292 (2023).

Zhou, B., Lu, B. & Zhang, Z. Placement of edge servers in mobile cloud computing using artificial bee colony algorithm. Int. J. Adv. Comput. Sci. Appl. 14 (2023).

Moorthy, R. S., Arikumar, K. S. & Prathiba, B. S. B. An improved whale optimization algorithm for optimal placement of edge server. In Chinara, S., Tripathy, A. K., Li, K.-C., Sahoo, J. P. & Mishra, A. K. (eds.) Advances in Distributed Computing and Machine Learning , 89–100 (Springer Nature Singapore, Singapore, 2023).

Zhang, X., Zhang, J., Peng, C. & Wang, X. Multimodal optimization of edge server placement considering system response time. ACM Transact. Sens. Netw. 19 , 1–20 (2022).

Kipf, T.N. & Welling, M. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907 (2016).

Passos, L. A., Papa, J. P., Del Ser, J., Hussain, A. & Adeel, A. Multimodal audio-visual information fusion using canonical-correlated graph neural network for energy-efficient speech enhancement. Inform. Fusion 90 , 1–11 (2023).

Tzirakis, P., Kumar, A. & Donley, J. Multi-channel speech enhancement using graph neural networks. In ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) , 3415–3419 (IEEE, 2021).

Sarlin, P.-E., DeTone, D., Malisiewicz, T. & Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition , 4938–4947 (2020).

Wu, Z. et al. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 32 , 4–24 (2020).

Article   MathSciNet   Google Scholar  

Kumar, V. S. et al. Natural language processing using graph neural network for text classification. In 2022 International Conference on Knowledge Engineering and Communication Systems (ICKES) , 1–5 (IEEE, 2022).

Zhang, W., Yang, X. & Li, J. Sensor placement for leak localization in water distribution networks based on graph convolutional network. IEEE Sens. J. 22 , 21093–21100. https://doi.org/10.1109/JSEN.2022.3208415 (2022).

Chen, Z., Zhu, B. & Zhou, C. Container cluster placement in edge computing based on reinforcement learning incorporating graph convolutional networks scheme. Digital Commun. Netw. (2023).

Ling, C. et al. An edge server placement algorithm based on graph convolution network. IEEE Transact. Veh. Technol. (2022).

Miao, W. et al. Workload prediction in edge computing based on graph neural network. In 2021 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom) , 1663–1666 (IEEE, 2021).

Wilder, B., Ewing, E., Dilkina, B. & Tambe, M. End to end learning and optimization on graphs 1905 , 13732 (2020).

Wang, S. et al. Delay-aware microservice coordination in mobile edge computing: A reinforcement learning approach. IEEE Trans. Mob. Comput. 20 , 939–951 (2021).

Download references

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China Project under Grant 62262064, Grant 62266043 and Grant 61966035; in part by the Key R&D projects in Xinjiang Uygur Autonomous Region under Grant XJEDU2016S106; in part by the Natural Science Foundation of Xinjiang Uygur Autonomous Region of China under Grant 2022D01C56; and in part by the Social Science Foundation of Xinjiang Uygur Autonomous Region of China under Grant 22BTQ067. We would also like to thank our tutor for the careful guidance and all the participants for their insightful comments.

Author information

Authors and affiliations.

School of Computer Science and Technology, Xinjiang University, Urumqi, 830046, China

Shanshan Zhang & Jiong Yu

Xinjiang Petroleum Engineering Co., Ltd, Karamay, 834000, China

Mingjian Hu

You can also search for this author in PubMed   Google Scholar

Contributions

S.S.Z. conceived the experiments, S.S.Z. and J.Y. conducted the experiments, M.J.H analysed the results. S.S.Z. wrote the main manuscript text. All authors reviewed the manuscript.

Corresponding author

Correspondence to Jiong Yu .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/ .

Reprints and permissions

About this article

Cite this article.

Zhang, S., Yu, J. & Hu, M. An edge server placement based on graph clustering in mobile edge computing. Sci Rep 14 , 29986 (2024). https://doi.org/10.1038/s41598-024-81684-5

Download citation

Received : 06 April 2024

Accepted : 28 November 2024

Published : 02 December 2024

DOI : https://doi.org/10.1038/s41598-024-81684-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Edge server placement
• Mobile edge computing
• Graph clustering
• Graph convolutional network

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.