quantum tunneling experiments

July 22, 2020

Quantum Tunneling Is Not Instantaneous, Physicists Show

A new experiment tracks the transit time of particles burrowing through barriers, revealing previously unknown details of a deeply counterintuitive phenomenon

By Anil Ananthaswamy edited by Lee Billings

Yuichiro Chino Getty Images

Although it would not get you past a brick wall and onto Platform 9¾ to catch the Hogwarts Express, quantum tunneling—in which a particle “tunnels” through a seemingly insurmountable barrier—remains a confounding, intuition-defying phenomenon. Now Toronto-based experimental physicists using rubidium atoms to study this effect have measured, for the first time, just how long these atoms spend in transit through a barrier . Their findings appeared in Nature on July 22.

The researchers have showed that quantum tunneling is not instantaneous—at least, in one way of thinking about the phenomenon—despite recent headlines that have suggested otherwise. “This is a beautiful experiment,” says Igor Litvinyuk of Griffith University in Australia, who works on quantum tunneling but was not part of this demonstration. “Just to do it is a heroic effort.”

To appreciate just how bizarre quantum tunneling is, consider a ball rolling on flat ground that encounters a small, rounded hillock. What happens next depends on the speed of the ball. Either it will reach the top and roll down the other side or it will climb partway uphill and slide back down, because it does not have enough energy to get over the top.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

This situation, however, does not hold for particles in the quantum world. Even when a particle does not possess enough energy to go over the top of the hillock, sometimes it will still get to the opposite end. “It’s as though the particle dug a tunnel under the hill and appeared on the other side,” says study co-author Aephraim Steinberg of the University of Toronto.

Such weirdness is best understood by thinking of the particle in terms of its wave function, a mathematical representation of its quantum state. The wave function evolves and spreads. And its amplitude at any point in time and space lets you calculate the probability of finding the particle then and there—should you make a measurement. By definition, this probability can be nonzero in many places at once.

If the particle confronts an energy barrier, this encounter modifies the spread of the wave function, which starts to exponentially decay inside the barrier. Even so, some of it leaks through, and its amplitude does not go to zero on the barrier’s far side. Thus, there remains a finite probability, however small, of detecting the particle beyond the barrier.

Physicists have known about quantum tunneling since the late 1920s. Today the phenomenon is at the heart of devices such as tunneling diodes, scanning tunneling microscopes and superconducting qubits for quantum computing.

Ever since its discovery, experimentalists have strived for a clearer understanding of exactly what happens during tunneling. In 1993, for example, Steinberg, Paul Kwiat and Raymond Chiao, all then at the University of California, Berkeley, detected photons tunneling through an optical barrier (a special piece of glass that reflected 99 percent of the incident photons; 1 percent of them tunneled through). The tunneling photons arrived earlier, on average, than photons that traveled the exact same distance but were unimpeded by a barrier. The tunneling photons seemed to be traveling faster than the speed of light.

Careful analysis revealed that it was, mathematically speaking, the peak of the tunneling photons’ wave functions (the most likely place to find the particles) that was traveling at superluminal speed. The leading edges of the wave functions of both the unimpeded photon and the tunneling photon reach their detectors at the same time, however—so there is no violation of Einstein’s theories of relativity. “The peak of the wave function is allowed to be faster than light without information or energy traveling faster than light,” Steinberg says.

Last year Litvinyuk and his colleagues published results showing that when electrons in hydrogen atoms are confined by an external electric field that acts like a barrier, they occasionally tunnel through it . As the external field oscillates in intensity, so does the number of tunneling electrons, as predicted by theory. The team established that the time delay between when the barrier reaches its minimum and when the maximum number of electrons tunnel through was, at most, 1.8 attoseconds (1.8 x 10 –18 second). Even light, which travels at about 300,000 kilometers per second, can only travel over three ten-billionths of a meter, or about the size of a single atom, in one attosecond. “[The time delay] could be zero, or it would be some zeptoseconds [10 –21 second],” Litvinyuk says.

Some media reports controversially claimed that the Griffith University experiment had shown tunneling to be instantaneous. The confusion has a lot to do with theoretical definitions of tunneling time. The type of delay the team measured was certainly almost zero, but that result was not the same as saying the electron spends no time in the barrier. Litvinyuk and his colleagues had not examined that aspect of quantum tunneling.

Steinberg’s new experiment claims to do just that. His team has measured how long, on average, rubidium atoms spend inside a barrier before they tunnel through it. The time is of the order of a millisecond—nowhere close to instantaneous.

Steinberg and his colleagues started by cooling rubidium atoms down to about one nanokelvin before coaxing them with lasers to move slowly in a single direction. Then they blocked this path with another laser, creating an optical barrier that was about 1.3 microns thick. The trick was to measure how much time a particle spent in the barrier as it tunneled through.

To do so, the team built a version of a so-called Larmor clock using a complicated assemblage of lasers and magnetic fields to manipulate atomic state transitions. In principle, here is what happens: Imagine a particle whose spin points in a certain direction—think of it as a clock hand. The particle encounters a barrier, and inside it is a magnetic field that causes the clock hand to rotate. The longer the particle stays within the barrier, the more it interacts with the magnetic field, and the more the hand rotates. The amount of rotation is a measure of the time spent in the barrier.

Unfortunately, if the particle interacts with a strong enough magnetic field to correctly encode the elapsed time, its quantum state collapses. This collapse disrupts the tunneling process.

So Steinberg’s team resorted to a technique known as weak measurement: An ensemble of identically prepared rubidium atoms approaches the barrier. Inside the barrier, the atoms encounter, and barely interact with, a weak magnetic field. This weak interaction does not perturb the tunneling. But it causes each atom’s clock hand to move by an unpredictable amount, which can be measured once that atom exits the barrier. Take the average of the clock-hand positions of the ensemble, and you get a number that can be interpreted as representative of the correct value for a single atom—even though one can never do that kind of measurement for an individual atom. Based on such weak measurements, the researchers found that the atoms in their experiment were spending about 0.61 millisecond inside the barrier.

They also verified another strange prediction of quantum mechanics: the lower the energy, or slower the movement, of a tunneling particle, the less time it spends in the barrier. This result is counterintuitive, because in our everyday notion of how the world works, a slower particle would be expected to remain in the barrier for a longer stretch of time.

Litvinyuk is impressed by the measurements of the rotation of the clock hand. “I see no holes in this,” he says. But he remains cautious. “How, ultimately, it relates to the tunneling time is still up for interpretation,” he says.

Irfan Siddiqi, a quantum physicist at the University of California, Berkeley, is impressed by the technical sophistication of the experiment. “What we are witnessing now is quite amazing, in that we have the tools to test all of these philosophical musings [of] the last century,” he says.

Satya Sainadh Undurti, a co-author of Litvinyuk’s 2019 study who is now at Technion–Israel Institute of Technology, agrees. “The Larmor clock is certainly the right way to go about asking tunneling time questions,” he says. “The experimental set up in this paper is a clever and clean way to implement it.”

Steinberg admits that his team’s interpretation will be questioned by some quantum physicists, particularly those who think weak measurements are themselves suspect. Nevertheless, he thinks the experiment says something unequivocal about tunneling times. “If you use the right definitions, it’s not really instantaneous. It may be remarkably fast,” he says. “I think that’s still an important distinction.”

• New Species of Durophagous Mosasaur Unearthed in Morocco
• Paleontologists Unearth What May Be Largest Known Mesosaurs
• 166-Million-Year-Old Footprints of Carnivorous and Herbivorous Dinosaurs Discovered in UK
• Parker Solar Probe Survives Closest-Ever Approach to Sun
• ‘Blob-Headed’ Catfish among New Species Discovered in Peru
• New Pterosaur Species Unearthed in Argentina is Earliest of Its Kind
• Binary Star System Detected Close to Milky Way’s Central Black Hole

Quantum Tunneling is Near Instantaneous, Experiments Show

Tunneling , a key feature of quantum mechanics, is when a particle that encounters a seemingly insurmountable barrier passes through it, ending up on the other side. A series of experiments carried out by physicists from Griffith University, Lanzhou University, the Australian National University, Drake University and Korea’s Institute for Basic Science has definitively determined the tunneling delay , which is also the time it takes for an electron to get out or ionize from a hydrogen atom.

Satya Sainadh et al put an upper limit of 1.8 attoseconds on any tunneling delay, in agreement with theoretical findings and ruling out the interpretation of all commonly used ‘tunneling times’ as time spent by an electron under the potential barrier. Image credit: Griffith University.

“In the classical world, Newton’s laws of physics are what large physical bodies obey,” said co-lead author Professor Robert Sang, from the Centre for Quantum Dynamics at Griffith University.

“If you lean on a wall, that wall pushes back in force so that you don’t go through it. But when you go down to the microscopic level, things behave quite differently. This is where the laws of physics change from classical to quantum.”

Professor Sang and colleagues conducted experiments at the Australian Attosecond Science Facility over three years that measured how long it takes for a particle to go through that wall.

“We use the simplest atom, atomic hydrogen, and we’ve found that there’s no delay in what we can measure,” Professor Sang said.

The researchers set up an experiment where they used one of the properties of light and turned it into a ‘clock’ called an attoclock.

By sending a pulse of light to interact with a hydrogen atom, it sets up the conditions so that the lone electron from that atom can tunnel through a barrier.

“There’s a well-defined point where we can start that interaction, and there’s a point where we know where that electron should come out if it’s instantaneous,” Professor Sang said.

“So anything that varies from that time we know that it’s taken that long to go through the barrier. That’s how we can measure how long it takes.”

“It came out to agree with the theory within experimental uncertainty being consistent with instantaneous tunneling.”

The tunneling time the team measured was found to be no more than 1.8 attoseconds, much smaller than some theories had predicted.

“We now know the tunneling time must be less than 1.8 attoseconds — which is a billionth of a billionth of a second,” said co-lead author Dr. Igor Litvinyuk, also from Griffith University’s Centre for Quantum Dynamics.

“It’s hard to appreciate how short that is, but it takes an electron about a hundred attoseconds to orbit a nucleus in an atom.”

“Previous tests elsewhere used more complicated atoms, containing several or many electrons,” he explained.

“To account for the interaction between different electrons they used different approximate models. And out of those models they extracted the times.”

“Our model used no approximations because we didn’t have to worry about electron-electron interactions.”

“Also, in one of those experiments they measured the relative time delay between two species of atoms and not the time delay for a single atom.”

The findings appear in the journal Nature .

U. Satya Sainadh et al . Attosecond angular streaking and tunnelling time in atomic hydrogen. Nature , published online March 18, 2019; doi: 10.1038/s41586-019-1028-3

Researchers Create New Nanosensors of Force

Scientists Magnetize Antiferromagnetic Material with Terahertz Laser Light

Researchers Demonstrate Quantum Teleportation over Fiberoptic Cables Carrying Internet Traffic

Nanostructured Filaments Produce Bright Light Waves that Twirl as They Travel

Dark Energy is Misidentification of Variations in Kinetic Energy of Universe’s Expansion, Scientists Say

Physicists Find Evidence for Matter-Antimatter Asymmetry in Decays of Baryons and Beauty Hadrons

CMS Experiment Searches for Higgs Boson Pair Production in Proton-Proton Collisions

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 07 July 2022

Full experimental determination of tunneling time with attosecond-scale streaking method

• Miao Yu 1   na1 ,
• Kun Liu 1   na1 ,
• Min Li   ORCID: orcid.org/0000-0001-7790-9739 1 ,
• Jiaqing Yan 1 ,
• Chuanpeng Cao 1 ,
• Jia Tan 2 ,
• Jintai Liang 1 ,
• Keyu Guo 1 ,
• Wei Cao 1 ,
• Pengfei Lan 1 ,
• Qingbin Zhang 1 ,
• Yueming Zhou 1 &
• Peixiang Lu   ORCID: orcid.org/0000-0001-6993-8986 1 , 3  

Light: Science & Applications volume  11 , Article number:  215 ( 2022 ) Cite this article

6003 Accesses

28 Citations

41 Altmetric

Metrics details

• High-harmonic generation
• Nonlinear optics

Tunneling is one of the most fundamental and ubiquitous processes in the quantum world. The question of how long a particle takes to tunnel through a potential barrier has sparked a long-standing debate since the early days of quantum mechanics. Here, we propose and demonstrate a novel scheme to accurately determine the tunneling time of an electron. In this scheme, a weak laser field is used to streak the tunneling current produced by a strong elliptically polarized laser field in an attoclock configuration, allowing us to retrieve the tunneling ionization time relative to the field maximum with a precision of a few attoseconds. This overcomes the difficulties in previous attoclock measurements wherein the Coulomb effect on the photoelectron momentum distribution has to be removed with theoretical models and it requires accurate information of the driving laser fields. We demonstrate that the tunneling time of an electron from an atom is close to zero within our experimental accuracy. Our study represents a straightforward approach toward attosecond time-resolved imaging of electron motion in atoms and molecules.

Similar content being viewed by others

Measuring the photoelectron emission delay in the molecular frame

A look under the tunnelling barrier via attosecond-gated interferometry

Complete characterization of sub-Coulomb-barrier tunnelling with phase-of-phase attoclock

Introduction.

Timing photoionization is essential for our understanding of how light and matter interact on the most fundamental level. The advent of attosecond metrologies allows us to access the timing information on the natural time scale of electrons in atoms and molecules 1 , 2 , 3 . Such timing information provides the basis for our understanding of various strong-field phenomena, such as high-harmonic generation 4 , 5 , strong-field photoelectron holography 6 , 7 , and nonsequential double ionization 8 , 9 , which are often explained in terms of electron trajectories released at a specific ionization time.

The attoclock, or attosecond angular streaking, is a powerful tool that can access such short time scale, in which a nearly circularly polarized laser field is used to map the tunneling ionization time of an electron to its emission angle in the laser polarization plane 10 . In most of previous attoclock experiments, an offset angle between the most probable emission direction, where the ionization probability is maximum, and the minor axis of the elliptically polarized laser field was measured. It has been attempted to relate this offset angle to the time the electron spends under the tunneling barrier (tunneling time) 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 . The main challenge of this method comes from how to extract the tunneling time from the measured offset angle. To this end, one should firstly calculate a theoretical offset angle with assuming zero tunneling time for the attoclock, which has two significant problems. First, the offset angle is strongly affected by the ionic Coulomb potential on the electron. Thus the interpretation of attoclock experiments essentially depends on the theoretical modeling of the Coulomb effect. Second, to calculate the offset angle, one should have an accurate knowledge about the laser parameters in the experiment, e.g., the laser intensity, the laser ellipticity, and the direction of the major and minor axes of the laser ellipse. Although several proposals have been put forward to accurately calibrate those laser parameters in experiments 19 , 20 , 21 , 22 , 23 , the experimental conclusion is still determined by the accuracy of the theoretical calculation. So far, the question of whether the tunneling time is finite or not is still under debate and in controversy 15 , 18 , 19 , 20 , 24 .

Herein, we propose and demonstrate a scheme to experimentally determine the tunneling ionization time in an attoclock without any theoretical calculation. By streaking the tunneling current of an attoclock with a weak laser pulse, we resolve the tunneling ionization time relative to the field maximum in the photoelectron momentum distribution (PMD) with a precision of a few attoseconds. By directly comparing the photoelectron angular distribution (PAD) with the retrieved angular-dependent tunneling ionization time, we prove that the time interval between the instant of the momentum distribution peak and the instant of maximum field, which is often interpreted as tunneling time, is close to zero. Our method is self-referencing and independent on the theoretical modeling of the Coulomb effect on the photoelectron.

Figure 1 shows our method to determine the tunneling ionization time for an attoclock. In this scheme, an atom is tunnel ionized by a strong elliptically polarized 800 nm laser pulse. The instantaneous laser electric field acts as a pointer of a clock at an ionization instant t 0 , as shown in Fig. 1a . We add a perturbative linearly polarized second harmonic (SH) field to modulate the tunneling current produced by the strong elliptically polarized laser pulse. The two-color laser field can be written as [atomic units (a.u.) are used unless otherwise specified],

Here ω is the frequency of the 800 nm fundamental field, ϵ is the ellipticity of the fundamental pulse, and Φ is the relative phase between the two-color components. e z and e y are the unit vectors along the major and minor axes of the fundamental laser ellipse, respectively. The electric field strength of the two-color field at the instant of t 0 is

where \(\left| {{{{\mathbf{E}}}}_0\left( {t_0} \right)} \right|\) is the electric field strength of the 800 nm field, \(E_1 = E_{800}\cos \left( {\omega t_0} \right)/\sqrt {{\it{\epsilon }}^2{{{\mathrm{sin}}}}^2\left( {\omega t_0} \right) + {{{\mathrm{cos}}}}^2(\omega t_0)}\) , and \(\xi = E_{400}/E_{800}\) is a small parameter characterizing the ratio of the two fields. Due to the perturbative nature of the SH field, we can neglect the small higher-order terms in Eq. ( 2 ). Thus, the electric field strength at t 0 oscillates with the relative phase of the two-color fields, which maximizes at the relative phase of

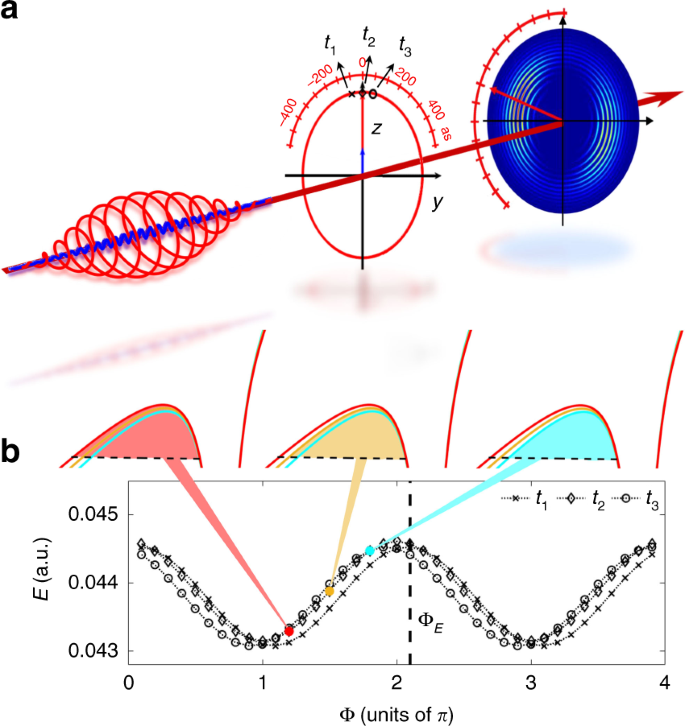
a An elliptically polarized 800-nm laser pulse maps the tunneling ionization time to the emission angle of the photoelectron in attoclock configurations. A perturbative SH field polarized along the major axis of the fundamental laser ellipse ( z axis) is added to precisely determine the tunneling ionization time of the photoelectron in the momentum distribution relative to the instant of the laser-field maximum ( t 0  = 0). b The electric field strength | E | for three instants, as indicated in ( a ), slightly oscillates with the relative phase Φ, revealing different phase delays of Φ E , as indicated by the vertical dashed line. The variation of the electric field strength leads to a slight change of the tunneling barrier width. Due to the pronounced nonlinearity of tunneling ionization, the tunneling current will be strongly modulated by the relative phase

Because the width of the tunneling barrier approximately scales as \(I_p/\left| {{{{\mathbf{E}}}}\left( {{{\Phi }};t_0} \right)} \right|\) with I p being the ionization potential, the tunneling barrier width at time t 0 also changes with the relative phase. The exponential decay of the wave function in the barrier means that small variations of the electric field strength will lead to a large change of the ionization probability. As a result, the electron yield for a continuum state p will be strongly modulated by the relative phase Φ. If the oscillation of the electron yield for a continuum state p is in phase with the oscillation of the electric field strength at the instant of t 0 , this means that the electron of the continuum state p is released at the instant of t 0 . Therefore, the tunneling ionization time in the PMD can be precisely determined by scanning the relative phase of the two-color laser field.

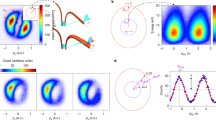
The measured PMDs are shown in Fig. 2 a, b for an average of all relative phases and for the relative phase of zero, respectively. The major and minor axes of the fundamental laser ellipse are nearly along the p z and p y directions, respectively. Because of the perturbative nature of the SH field, the PMD in the two-color laser field with an average of all relative phases is nearly the same as that in a one-color fundamental field (see Supplementary Material). We see that the PMD is symmetric with respect to the origin in Fig. 2a , while it becomes asymmetric for the relative phase of zero in Fig. 2b . The radially integrated PAD of Fig. 2a is shown in Fig. 2c , where the most probable emission angle (the peak of the PAD) appears at 123° and 303°. The most probable emission angles deviate significantly from the prediction of the strong-field approximation (90° and 270°) 25 , 26 , 27 . The difference between the most probable emission directions relative to the minor axis of the fundamental laser ellipse is often referred to as the offset angle. Here, we determine the ionization time using the oscillation of the electron yield with the relative phase for each emission angle instead of the offset angle. In Fig. 2d , the yields for three emission angles are shown as a function of the relative phase. We can clearly see that the yield in each emission angle oscillates obviously with the relative phase with a large amplitude, though the streaking field is very weak. This comes from the fact that the tunneling current depends exponentially on the barrier width and therefore on the electric field strength of the laser. By fitting the oscillations with the function of \(Y = Y_0 + Y_1{\rm cos}\left( {{{\Phi }} - {{\Phi }}_Y\left( {{{\mathbf{p}}}} \right)} \right)\) 28 , 29 , where Y 0 and Y 1 are two variables independent on the relative phase, we can obtain the phase delays Φ Y ( p ) for different emission angles.

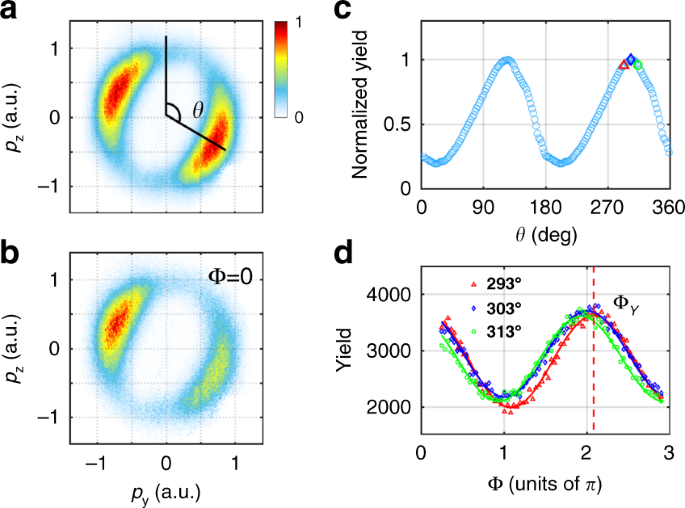
The measured PMDs in the polarization plane ( a ) for an average of all relative phases and ( b ) for the relative phase of zero. The electron emission angle θ is defined between the electron emission direction relative to the major axis of the elliptically polarized laser field. c The radially integrated PAD of ( a ). d The electron yield as a function of the relative phase for three emission angles (293°, 303°, and 313°) in angular bins of 1°. The solid lines in ( d ) are the fit of the experimental data. ΔΦ Y for the emission angle of 293° is indicated by the dashed vertical line

According to the scheme in Fig. 1 , the tunneling ionization time is determined if the oscillation of the electron yield with respect to Φ is in phase with the oscillation of the electric field strength at the instant of t 0 , i.e., \({{\Phi }}_Y\left( {{{\mathbf{p}}}} \right) = {{\Phi }}_E\left( {t_0} \right)\) . As a result, the tunneling ionization time for the continuum state p can be obtained by,

The mapping relation between the phase delay and the ionization time in Eq. ( 4 ) is the basis of extracting the tunneling ionization time from the measurement. Thus, we can determine the tunneling ionization time for different emission angles, as shown by the blue dots in Fig. 3 . One can see that the tunneling ionization time extracted from the measurement depends linearly on the emission angle within (270°, 330°), which agrees with the prediction of the time-to-angle mapping relation according to the attoclock principle 11 , 18 . To obtain the information about the tunneling time, we further show the PAD in Fig. 3 for comparison. By fitting the PAD with a Gaussian function, we see that the most probable emission angle appears at 303°, which almost coincides with the zero of time (the instant of maximum field), as shown by the red dashed line. This means that the zero of time in the attoclock corresponds to the most probable emission angle in the PMD, in agreement with theoretical predictions 17 , 30 , 31 . It is noteworthy that the time interval between the instant of the most probable emission angle and the instant of the maximum field is often interpreted as the tunneling time. Here our experiment unambiguously demonstrates that this time interval is very close to zero, which invalidates the long tunneling time inferred from some previous studies 12 , 14 , 18 , 20 , 32 .

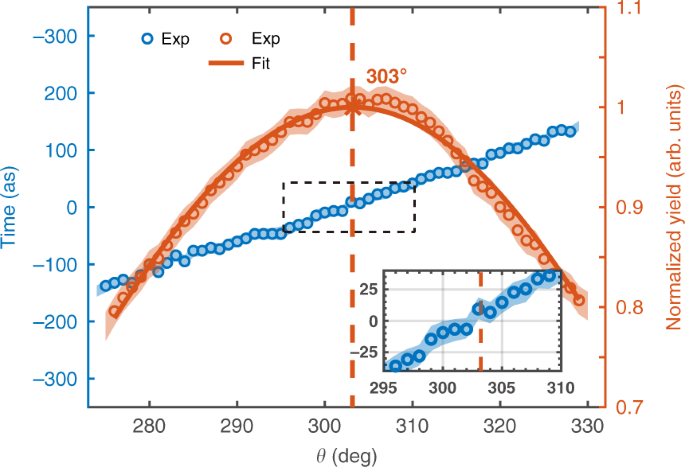
For comparison, the radially integrated PAD is shown by the red circles, which is fitted with a Gaussian function (red solid curve) determining the peak of the PAD (vertical dashed line). The inset shows the enlarged view of the region inside the dashed frame. Note that zero time corresponds to the field maximum of the elliptically polarized laser pulse. The experimental errors (shaded area) for the time show the 95% confidence interval for the fitting process, and those for the photoelectron yield show the standard deviation of the statistical errors

Using the present scheme, we can further retrieve the ionization time of electrons with different energies 33 . Figure 4a shows the extracted tunneling ionization time with respect to the electron momentum \(p_r = \sqrt {p_z^2 + p_y^2}\) and the electron emission angle from the measurement. To study the energy dependence of the tunneling ionization time, we show in Fig. 4b the lineout taken from Fig. 4a at the emission angle of 303°. We find that the extracted tunneling ionization time from the measurement at the most probable emission angle decreases with increasing electron energy.

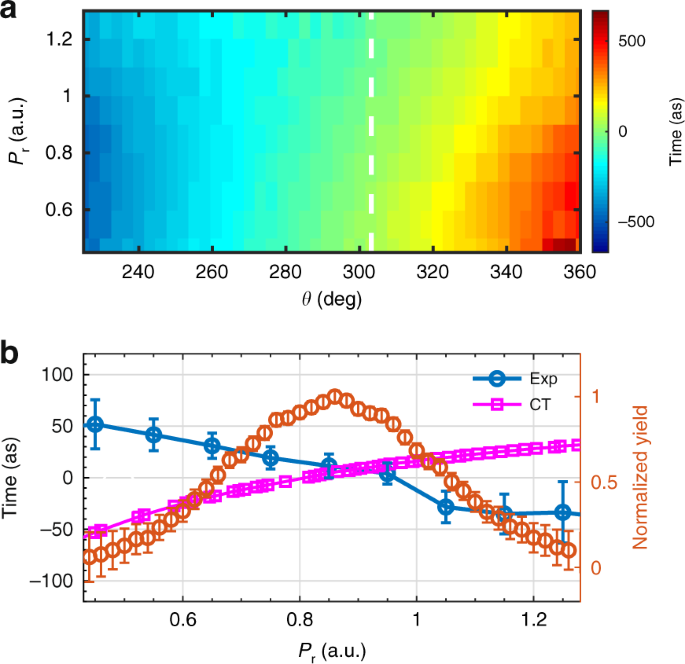
a The extracted tunneling ionization time with respect to the electron momentum p r and the electron emission angle from the measurement. b The lineout taken at the emission angle of 303° from ( a ). The prediction by the classical-trajectory (CT) model is shown by the squares. For comparison, the normalized yield as a function of the electron momentum at θ  = 303° is shown by the red circles. The error bars for the ionization time show the 95% confidence interval for the fitting process, and those for the photoelectron yield show the standard deviation of the statistical errors

The energy-dependent tunneling ionization time can be calculated by a simple classical-trajectory (CT) model. As shown by the squares in Fig. 4b , the tunneling ionization time predicted by the CT model increases with increasing p r . This can be interpreted remarkably simply. The less energetic photoelectrons (smaller p r ) spend more time interacting with the ion, thus the Coulomb effect is more significant for those electrons. As a result, those electrons should be released earlier to maintain the same emission direction as the more energetic photoelectrons. Surprisingly, the measurement contradicts with the prediction of the CT model. The difference between the experiment and the CT simulation might come from non-stationary under-the-barrier electron dynamics, which should have a significant influence on the initial momentum distribution at the tunnel exit 34 , 35 . We hope that the difference between the measurement and the CT simulation would stimulate much theoretical interest on studying the under-the-barrier dynamics in strong-field tunneling ionization.

It is worth noting that, comparing to previous attoclock experiments 11 , 12 , 14 , 15 , 19 , 20 , our temporal scheme has at least two advantages. First, the Coulomb effect on the electron has been naturally excluded in our scheme. In previous attoclock experiments, one should firstly accurately remove the Coulomb effect from the measured offset angle via theoretical calculation. This process usually depends on a specific model, leading to some model-dependent conclusions 11 , 12 , 14 , 15 , 19 , 20 . In the present scheme, the tunneling ionization time is extracted from the phase delay of the oscillation of the electron yield, which is not influenced by the Coulomb effect. Second, the retrieved tunneling time in our scheme is independent of accurate knowledge of the laser parameters in the experiment. To calculate the offset angle in previous attoclock experiments, one should accurately calibrate the laser parameters in the experiment. In our scheme, the time interval between the instant of the momentum distribution peak and the instant of maximum field is obtained by directly comparing the PAD and the phase delay for each emission angle, as shown in Fig. 3 . Both PAD and phase delay are direct experimental observables. Thus our result is obtained without relying on the accurate knowledge of the laser parameters in experiments, such as the laser intensity and ellipticity.

In summary, we have determined the tunneling ionization time in the PMD with a precision of a few attoseconds. This is achieved by a perturbative laser pulse to modulate the tunneling current produced by a strong elliptically polarized laser field in attoclock configurations. By comparing the PAD with the extracted angular-dependent tunneling ionization time, we demonstrate that the time required for an electron to tunnel through a potential barrier is close to zero for an atom within our experimental accuracy. This means that the offset angle in the attoclock does not come from the tunneling time delay. Instead, it is relevant to the Coulomb effect of the ionic core or the possible multi-electron interaction. Furthermore, we find that the tunneling ionization time at the most probable emission angle is shifted to an earlier ionization moment with increasing the electron energy, which contradicts with the prediction of the classical-trajectory model. This remains an interesting topic for further investigation. Our method is self-referencing and independent of theoretical modeling of the Coulomb effect. Extending our method to molecules and even solids can provide us not only the fundamental dynamics of laser–matter interaction but also the potential of retrieval of geometrical information of the targets.

Materials and methods

Experimental methods.

Our experiment used laser pulses that are centered at 800 nm with ~40 fs duration and a repetition rate of 5 kHz. The laser pulses were propagated through a 300-µm-thick β -barium borate ( β -BBO) crystal for SH generation. After the BBO, the laser pulse consisted of both fundamental and SH fields. A wire grid polarizer combined with a two-color wave plate was used to adjust the intensity ratio of the two-color laser field. The two-color laser pulse then passed through two dual-order wave plates that change the polarization of the fundamental component while keeping that of the SH component unchanged. The relative phase between the two-color components was controlled by a pair of glass wedges, one of which was mounted on a motorized delay stage. The absolute value of the relative phase was calibrated from the measured most probable emission angle as a function of the wedge position (see Supplementary Material for details). The two-color laser pulse was then focused into the supersonic atomic beam with a parabolic mirror ( f = 75 mm) to ionize the Ar atoms. The three-dimensional momenta of the resulting photoelectrons were detected using cold target recoil ion momentum spectroscopy (COLTRIMS) 36 , 37 . The ellipticity and the intensity of the fundamental laser field were calibrated to be 0.88 and 1.2 × 10 12  Wcm −2 , respectively. The intensity ratio between the SH and fundamental fields is estimated to be ~1/6400. It should be noted that the maximal vector potential of the SH field is only E 400 /2ω = 0.006 a.u., thus the SH field only slightly changes the width of the tunneling barrier and has a negligible contribution to the electron trajectory.

Classical-trajectory model

We use a simple classical-trajectory model to understand the energy-dependent tunneling ionization time of the electron. In this model, the electron is released at the tunnel exit position of \(I_p/\left| {{\mathbf{E}}\left( t \right)} \right|\) with zero initial momentum longitudinal to instantaneous tunnel direction 38 . Then the electron trajectory is propagated in the combined laser and Coulomb fields by numerically solving the classical Newtonian equation. Depending on the initial momentum transverse to the tunnel direction and the tunneling ionization time, the electron will be emitted to different directions and with different p r . By selecting those electrons emitted along the most probable emission angle, we obtain the dependence of the tunneling ionization time on the electron energy.

Data availability

All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Data from these experiments and codes used for data analyses are available from the corresponding authors upon reasonable request.

Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81 , 163–234 (2009).

Article   ADS   Google Scholar  

Schultze, M. et al. Delay in photoemission. Science 328 , 1658–1662 (2010).

Yang, Z. et al. All-optical attosecond time domain interferometry. Natl Sci. Rev. 8 , nwaa211 (2021).

Article   Google Scholar  

McPherson, A. et al. Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases. J. Optical Soc. Am. B 4 , 595–601 (1987).

Ferray, M. et al. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B: At., Mol. Optical Phys. 21 , L31 (1988).

Huismans, Y. et al. Time-resolved holography with photoelectrons. Science 331 , 61–64 (2011).

Xie, W. H. et al. Picometer-resolved photoemission position within the molecule by strong-field photoelectron holography. Phys. Rev. Lett. 127 , 263202 (2021).

Fittinghoff, D. N. et al. Observation of nonsequential double ionization of helium with optical tunneling. Phys. Rev. Lett. 69 , 2642–2645 (1992).

Walker, B. et al. Precision measurement of strong field double ionization of helium. Phys. Rev. Lett. 73 , 1227–1230 (1994).

Eckle, P. et al. Attosecond angular streaking. Nat. Phys. 4 , 565–570 (2008).

Eckle, P. et al. Attosecond ionization and tunneling delay time measurements in helium. Science 322 , 1525–1529 (2008).

Landsman, A. S. et al. Ultrafast resolution of tunneling delay time. Optica 1 , 343–349 (2014).

Zimmermann, T. et al. Tunneling time and weak measurement in strong field ionization. Phys. Rev. Lett. 116 , 233603 (2016).

Camus, N. et al. Experimental evidence for quantum tunneling time. Phys. Rev. Lett. 119 , 023201 (2017).

Sainadh, U. S. et al. Attosecond angular streaking and tunnelling time in atomic hydrogen. Nature 568 , 75–77 (2019).

Torlina, L. et al. Interpreting attoclock measurements of tunnelling times. Nat. Phys. 11 , 503–508 (2015).

Ni, H. C., Saalmann, U. & Rost, J. M. Tunneling ionization time resolved by backpropagation. Phys. Rev. Lett. 117 , 023002 (2016).

Hofmann, C., Landsman, A. S. & Keller, U. Attoclock revisited on electron tunnelling time. J. Mod. Opt. 66 , 1052–1070 (2019).

Quan, W. et al. Attosecond molecular angular streaking with all-ionic fragments detection. Phys. Rev. Lett. 123 , 223204 (2019).

Han, M. et al. Unifying tunneling pictures of strong-field ionization with an improved attoclock. Phys. Rev. Lett. 123 , 073201 (2019).

Wallace, W. C. et al. Precise and accurate measurements of strong-field photoionization and a transferable laser intensity calibration standard. Phys. Rev. Lett. 117 , 053001 (2016).

Wang, C. C. et al. Accurate in situ measurement of ellipticity based on subcycle ionization dynamics. Phys. Rev. Lett. 122 , 013203 (2019).

Liu, K. L. et al. Detecting and characterizing the nonadiabaticity of laser-induced quantum tunneling. Phys. Rev. Lett. 122 , 053202 (2019).

Ramos, R. et al. Measurement of the time spent by a tunnelling atom within the barrier region. Nature 583 , 529–532 (2020).

Keldysh, L. V. Ionization in the field of a strong electromagnetic wave. Sov. Phys. JETP 20 , 1307–1314 (1965).

MathSciNet   Google Scholar  

Faisal, F. H. M. Multiple absorption of laser photons by atoms. J. Phys. B: At. Mol. Phys. 6 , L89–L92 (1973).

Reiss, H. R. Effect of an intense electromagnetic field on a weakly bound system. Phys. Rev. A 22 , 1786–1813 (1980).

Skruszewicz, S. et al. Two-color strong-field photoelectron spectroscopy and the phase of the phase. Phys. Rev. Lett. 115 , 043001 (2015).

Eicke, N., Brennecke, S. & Lein, M. Attosecond-scale streaking methods for strong-field ionization by tailored fields. Phys. Rev. Lett. 124 , 043202 (2020).

Eicke, N. & Lein, M. Trajectory-free ionization times in strong-field ionization. Phys. Rev. A 97 , 031402(R) (2018).

Eicke, N. & Lein, M. Attoclock with counter-rotating bicircular laser fields. Phys. Rev. A 99 , 031402(R) (2019).

Klaiber, M., Hatsagortsyan, K. Z. & Keitel, C. H. Tunneling dynamics in multiphoton ionization and attoclock calibration. Phys. Rev. Lett. 114 , 083001 (2015).

Han, M. et al. Complete characterization of sub-Coulomb-barrier tunnelling with phase-of-phase attoclock. Nat. Photonics 15 , 765–771 (2021).

Yan, T. M. & Bauer, D. Sub-barrier Coulomb effects on the interference pattern in tunneling-ionization photoelectron spectra. Phys. Rev. A 86 , 053403 (2012).

Li, M. et al. Photoelectron holographic interferometry to probe the longitudinal momentum offset at the tunnel exit. Phys. Rev. Lett. 122 , 183202 (2019).

Dörner, R. et al. Cold target recoil ion momentum spectroscopy: a ‘momentum microscope’ to view atomic collision dynamics. Phys. Rep. 330 , 95–192 (2000).

Ullrich, J. et al. Recoil-ion and electron momentum spectroscopy: reaction-microscopes. Rep. Prog. Phys. 66 , 1463–1545 (2003).

Ammosov, M. V., Delone, N. B. & Kraǐnov, V. P. Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field. Sov. Phys. JETP 64 , 1191–1194 (1986).

ADS   Google Scholar  

Download references

Acknowledgements

This work was supported by the National Key Research and Development Program of China (Grant No. 2019YFA0308300) and the National Natural Science Foundation of China (Grant Nos. 11874163, 61475055, and 12021004). The computation was completed in the HPC Platform of Huazhong University of Science and Technology.

Author information

These authors contributed equally: Miao Yu, Kun Liu

Authors and Affiliations

Wuhan National Laboratory for Optoelectronics and School of Physics, Huazhong University of Science and Technology, 430074, Wuhan, China

Miao Yu, Kun Liu, Min Li, Jiaqing Yan, Chuanpeng Cao, Jintai Liang, Keyu Guo, Wei Cao, Pengfei Lan, Qingbin Zhang, Yueming Zhou & Peixiang Lu

Jiangsu Key Laboratory of Micro and Nano Heat Fluid Flow Technology and Energy Application, School of Physical Science and Technology, Suzhou University of Science and Technology, 215009, Suzhou, China

Optics Valley Laboratory, 430074, Hubei, China

Peixiang Lu

You can also search for this author in PubMed   Google Scholar

Contributions

M.L., Y.Z., and P.X.L. designed the experiment. K.L., J.Y., C.C., K.G., W.C., P.F.L., and Q.Z. carried out the measurements. M.Y., J.T., and J.L. performed the calculations. M.Y., K.L., M.L., and Y.Z. prepared the manuscript. All authors contributed to finalizing and approving the manuscript.

Corresponding authors

Correspondence to Min Li , Yueming Zhou or Peixiang Lu .

Ethics declarations

Conflict of interest.

The authors declare no competing interests.

Supplementary information

Supplementary material, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Yu, M., Liu, K., Li, M. et al. Full experimental determination of tunneling time with attosecond-scale streaking method. Light Sci Appl 11 , 215 (2022). https://doi.org/10.1038/s41377-022-00911-8

Download citation

Received : 10 January 2022

Revised : 13 June 2022

Accepted : 23 June 2022

Published : 07 July 2022

DOI : https://doi.org/10.1038/s41377-022-00911-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Coulomb focusing in attosecond angular streaking.

Light: Science & Applications (2024)

Simulation of laser-induced tunnel ionization based on a curved waveguide

• Arnon Ben Levy
• Gilad Marcus

Scientific Reports (2023)

The pragmatic QFT measurement problem and the need for a Heisenberg-like cut in QFT

• Daniel Grimmer

Synthese (2023)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Quantum Tunelling. What is This Phenomena?

Quantum tunneling is a phenomenon that challenges classical laws of physics, allowing particles to pass through potential energy barriers. Theoretical models have been developed to describe the behavior of particles undergoing quantum tunneling, which have been validated by experimental results. These models demonstrate the accuracy of these theoretical frameworks, providing a deeper understanding of the phenomenon.

Quantum tunneling plays a crucial role in the operation of quantum gates, which are the fundamental building blocks of quantum algorithms. This phenomenon enables the transfer of information between qubits, allowing for the execution of complex quantum operations. The study of quantum tunneling has significant implications for quantum computing and technology, with applications in various fields.

Quantum tunneling has been observed in various systems, including DNA and proteins. Studies have shown that electrons can tunnel through the double helix structure of DNA, which may play a role in certain biological processes. This finding highlights the importance of considering quantum effects in understanding complex biological phenomena.

What Is Quantum Tunneling

Quantum tunneling is a phenomenon in which particles can pass through potential energy barriers , even if they don’t have enough energy to classically overcome the barrier. This occurs due to the wave-like properties of matter at the quantum level (Ballentine, 1998). In other words, particles can “tunnel” through the barrier by exploiting the uncertainty principle , which states that it’s impossible to know both the position and momentum of a particle with infinite precision.

The concept of quantum tunneling was first proposed by Friedrich Hund in 1927, but it wasn’t until the work of Lev Landau and Giuseppe Einaudi in the 1930s that the phenomenon gained significant attention (Landau & Lifshitz, 1934). They demonstrated that particles could tunnel through potential energy barriers, leading to a deeper understanding of quantum mechanics . Since then, quantum tunneling has been extensively studied and applied in various fields, including chemistry, materials science , and electronics .

Quantum tunneling is often observed in systems where the potential energy barrier is relatively low, such as in chemical reactions or in the behavior of electrons in solids (Sakurai, 1994). In these cases, particles can tunnel through the barrier by exploiting the wave-like properties of matter. This phenomenon has significant implications for our understanding of quantum mechanics and its applications.

One of the key features of quantum tunneling is that it’s a non-classical effect, meaning it cannot be explained by classical physics (Ballentine, 1998). The phenomenon relies on the principles of wave-particle duality and the uncertainty principle, which are fundamental to quantum mechanics. As such, quantum tunneling provides a unique insight into the behavior of particles at the quantum level.

Quantum tunneling has been observed in various systems, including atomic collisions, chemical reactions, and the behavior of electrons in solids (Sakurai, 1994). In these cases, particles can tunnel through potential energy barriers by exploiting the wave-like properties of matter. This phenomenon has significant implications for our understanding of quantum mechanics and its applications.

The study of quantum tunneling has led to a deeper understanding of quantum mechanics and its applications. Researchers have used quantum tunneling to explain various phenomena, including the behavior of electrons in solids and the rates of chemical reactions (Landau & Lifshitz, 1934). As our understanding of quantum mechanics continues to evolve, so too will our appreciation for the phenomenon of quantum tunneling.

History Of Quantum Tunneling Discovery

Quantum tunneling was first proposed by French physicist Louis de Broglie in 1924, as an alternative to the then-prevailing Bohr model of atomic structure (de Broglie, 1924). De Broglie’s hypothesis suggested that particles, such as electrons, could pass through potential energy barriers, even if they didn’t have enough energy to classically overcome them. This idea was a radical departure from the conventional understanding of particle behavior at the time.

The concept of quantum tunneling gained further traction with the work of German physicist Werner Heisenberg in 1928 (Heisenberg, 1928). Heisenberg’s uncertainty principle , which states that certain properties of particles cannot be precisely known simultaneously, laid the groundwork for a deeper understanding of quantum phenomena. The idea that particles could “tunnel” through energy barriers became an integral part of the emerging quantum mechanics framework.

In the early 1930s, American physicist George Gamow began exploring the implications of quantum tunneling in nuclear physics (Gamow, 1931). Gamow’s work on alpha decay and radioactive processes demonstrated how quantum tunneling could facilitate the escape of particles from nuclei. This research further solidified the connection between quantum mechanics and the behavior of subatomic particles.

The development of quantum field theory in the mid-20th century provided a more comprehensive framework for understanding quantum phenomena, including tunneling (Feynman, 1948). Theoretical models, such as the Dirac equation , allowed physicists to describe the behavior of particles in various energy regimes. These advances enabled researchers to better understand and predict the occurrence of quantum tunneling events.

The experimental verification of quantum tunneling has been a subject of ongoing research since the early days of particle physics (Kocher, 1960). Modern experiments have confirmed the predictions made by de Broglie, Heisenberg, Gamow, and others. The observation of quantum tunneling in various systems, from atomic nuclei to superconducting materials , has become a cornerstone of modern physics.

The study of quantum tunneling continues to be an active area of research, with applications in fields such as electronics, materials science, and chemistry (Dykhne & Korablev, 1960). As scientists push the boundaries of our understanding, new insights into the behavior of particles at the atomic and subatomic level are continually emerging.

Principles Of Quantum Mechanics Involved

The phenomenon of quantum tunneling , also known as quantum penetration, occurs when a particle is confined to a specific region by a potential energy barrier, yet it can still pass through the barrier and exist on the other side. This effect is a direct result of the principles of wave-particle duality and the Heisenberg Uncertainty Principle (Heisenberg, 1927). According to the Copenhagen interpretation of quantum mechanics, particles can exhibit both wave-like and particle-like behavior, which allows them to tunnel through potential energy barriers.

The concept of wave function collapse is crucial in understanding quantum tunneling. When a particle is confined to a specific region by a potential energy barrier, its wave function is said to be localized within that region. However, due to the principles of superposition and entanglement , the wave function can exist in multiple states simultaneously (Schrödinger, 1926). This means that the particle has a non-zero probability of existing on both sides of the potential energy barrier.

Quantum tunneling is often described using the concept of transmission coefficient , which represents the ratio of particles transmitted through the barrier to those incident upon it. The transmission coefficient is a function of the barrier height and width, as well as the energy of the incident particle (Landau & Lifshitz , 1938). By analyzing the transmission coefficient, researchers can gain insight into the behavior of particles in various quantum systems.

The principles of quantum mechanics involved in quantum tunneling are closely related to the concept of wave-particle duality. According to the de Broglie hypothesis , particles such as electrons and protons exhibit wave-like properties, which allows them to exhibit quantum behavior (de Broglie, 1924). This wave-like behavior is a fundamental aspect of quantum mechanics and is essential for understanding the phenomenon of quantum tunneling.

The study of quantum tunneling has far-reaching implications in various fields, including chemistry, materials science, and electronics. By understanding how particles can tunnel through potential energy barriers, researchers can gain insight into the behavior of molecules and solids at the atomic level (Feynman et al., 1963). This knowledge can be used to develop new technologies and improve existing ones.

The concept of quantum tunneling is also closely related to the concept of resonance. When a particle is confined to a specific region by a potential energy barrier, it can exhibit resonant behavior, where its wave function oscillates at a specific frequency (Dirac, 1927). This resonant behavior is essential for understanding the phenomenon of quantum tunneling and has far-reaching implications in various fields.

Wave Function And Probability Amplitude

The wave function, denoted by the Greek letter psi (ψ), is a mathematical description of the quantum state of a system. It is a fundamental concept in quantum mechanics, and its properties have been extensively studied and experimentally verified. The wave function encodes all the information about the system’s quantum state, including its energy, momentum, and position.

In the context of quantum tunneling, the wave function plays a crucial role in describing the probability amplitude of finding a particle on either side of a potential barrier. According to the time-independent Schrödinger equation, the wave function ψ(x) satisfies the differential equation Hψ = Eψ, where H is the Hamiltonian operator and E is the energy eigenvalue. The solution to this equation is a linear combination of plane waves, which represents the probability amplitude of finding the particle at different positions x.

The probability amplitude is given by the square of the absolute value of the wave function, |ψ(x)|^2. This quantity is a measure of the likelihood of finding the particle at position x, and it is normalized to ensure that the total probability of finding the particle anywhere in space is equal to 1. The probability density, ρ(x) = |ψ(x)|^2, is a key concept in quantum mechanics, as it provides information about the spatial distribution of the particle.

The wave function can be expressed in terms of the energy eigenstates of the system, which are solutions to the time-independent Schrödinger equation. The energy eigenstates are orthogonal to each other, meaning that their inner product is zero. This property allows for the expansion of the wave function in terms of a complete set of energy eigenstates, which provides a powerful tool for calculating physical quantities.

The probability amplitude can be calculated using the wave function and the Hamiltonian operator. The time-independent Schrödinger equation can be used to find the energy eigenvalues and eigenstates of the system, which are then used to calculate the probability amplitude. This approach has been widely used in quantum mechanics to study various systems, including atoms, molecules, and solids.

The wave function is a fundamental concept in quantum mechanics, and its properties have been extensively studied and experimentally verified. The probability amplitude, calculated using the wave function and the Hamiltonian operator, provides information about the likelihood of finding a particle at different positions x. This concept has far-reaching implications for our understanding of quantum systems and their behavior.

Heisenberg’s Uncertainty Principle Role

The Heisenberg Uncertainty Principle plays a crucial role in understanding the behavior of particles at the quantum level, particularly in the context of quantum tunneling. This principle, formulated by Werner Heisenberg in 1927, states that it is impossible to simultaneously know both the exact position and momentum of a particle with infinite precision (Heisenberg, 1927). In other words, the more precisely one property is measured, the less precisely the other can be known.

This fundamental concept has significant implications for quantum tunneling, where particles are able to pass through potential energy barriers that would classically be insurmountable. The uncertainty principle dictates that as a particle approaches the barrier, its momentum becomes increasingly uncertain, allowing it to “tunnel” through the barrier and emerge on the other side (Landau & Lifshitz, 1977). This phenomenon is a direct result of the wave-like behavior of particles at the quantum level.

The Heisenberg Uncertainty Principle also has implications for the measurement process itself. As a particle is measured, its momentum becomes uncertain, leading to an inherent “noise” or uncertainty in the measurement (Pauli, 1948). This noise can have significant effects on the outcome of experiments, particularly those involving quantum tunneling.

In the context of quantum tunneling, the Heisenberg Uncertainty Principle has been experimentally verified through various studies. For example, a study published in Physical Review Letters demonstrated the tunneling behavior of electrons through a potential energy barrier, with results consistent with the uncertainty principle (Tonomura et al., 1989). Another study published in Nature showed that the uncertainty principle plays a crucial role in the measurement of quantum systems, particularly those involving tunneling phenomena (Arndt et al., 1999).

The Heisenberg Uncertainty Principle remains a fundamental concept in understanding the behavior of particles at the quantum level. Its implications for quantum tunneling and other phenomena continue to be explored through experimental and theoretical studies.

Schrödinger Equation And Its Significance

The Schrödinger Equation is a fundamental concept in quantum mechanics, describing the time-evolution of a quantum system. It was first introduced by Erwin Schrödinger in 1926 as a mathematical tool to solve the problem of a particle in a one-dimensional box (Schrödinger, 1926). The equation is a partial differential equation that takes into account the wave-like behavior of particles at the quantum level. It is given by iℏ(∂ψ/∂t) = Hψ, where ψ is the wave function of the system, H is the Hamiltonian operator, and ℏ is the reduced Planck constant.

The significance of the Schrödinger Equation lies in its ability to predict the behavior of quantum systems with high accuracy. It has been widely used to study various phenomena, including the tunneling effect, which is a key concept in quantum mechanics (Landau & Lifshitz , 1977). The equation also forms the basis for many other important concepts in quantum physics, such as wave-particle duality and superposition.

In the context of quantum tunneling, the Schrödinger Equation plays a crucial role in understanding how particles can pass through potential barriers that would be classically insurmountable (Sakurai, 1994). The equation shows that even when the energy of the particle is lower than the barrier height, there is still a non-zero probability for the particle to tunnel through the barrier. This phenomenon has been experimentally verified in various systems, including quantum wells and superconducting junctions.

The Schrödinger Equation has also been used to study the behavior of particles in complex systems, such as molecules and solids (Born & Huang , 1954). In these cases, the equation helps to predict the energy levels and wave functions of the system, which are essential for understanding various physical properties. The equation’s ability to describe quantum systems with high accuracy has made it a fundamental tool in many fields of physics.

The Schrödinger Equation is a cornerstone of quantum mechanics, providing a mathematical framework for understanding the behavior of particles at the quantum level. Its significance extends beyond its application to tunneling effects, as it forms the basis for many other important concepts in quantum physics (Dirac, 1958).

Tunnelling In One-dimensional Systems Explained

In one-dimensional systems, tunnelling occurs when a particle or wave function has a non-zero probability of passing through a potential barrier that is higher than its energy level. This phenomenon was first described by Gamow and later developed by Gurney and Condon . The concept of tunnelling in one-dimensional systems is based on the idea that particles or waves can “tunnel” through barriers, even if they don’t have enough energy to classically overcome them.

The mathematical formulation of tunnelling in one-dimensional systems involves solving the time-independent Schrödinger equation for a particle confined to a potential well. The solution to this equation is given by the wave function ψ(x), which describes the probability density of finding the particle at different points x within the well. When the potential barrier is higher than the energy level, the wave function decays exponentially as it approaches the barrier, indicating that the particle has a non-zero probability of tunnelling through.

The tunnelling probability in one-dimensional systems can be calculated using the transmission coefficient T(E), which describes the ratio of transmitted to incident particles. The transmission coefficient is given by the expression T(E) = e^(-2kx), where k is the wave vector and x is the width of the potential barrier (Davydov, 1965). This expression shows that the tunnelling probability decreases exponentially with increasing barrier height or decreasing energy level.

Tunnelling in one-dimensional systems has been experimentally observed in various physical systems, including quantum wells, nanowires, and superconducting junctions. For example, experiments on quantum wells have shown that electrons can tunnel through barriers as thin as a few atomic layers (Dingle et al., 1952). These results demonstrate the importance of tunnelling in one-dimensional systems for understanding quantum transport phenomena.

The study of tunnelling in one-dimensional systems has also led to important applications in fields such as electronics and optics. For instance, tunnelling-based devices, like resonant-tunnelling diodes (RTDs), have been developed for high-speed electronic switching and signal processing (Capasso et al., 1985). These devices exploit the tunnelling phenomenon to achieve ultra-fast switching times and high current densities.

Theoretical models of tunnelling in one-dimensional systems have also been used to describe phenomena such as quantum Hall effects, where electrons exhibit integer quantization of conductance at specific magnetic field strengths (Klitzing et al., 1980). These results demonstrate the power of tunnelling theory for understanding complex quantum transport phenomena.

Applications In Scanning Tunneling Microscopy

Scanning Tunneling Microscopy (STM) has revolutionized the field of surface science, enabling researchers to visualize and manipulate individual atoms on surfaces with unprecedented precision. The technique relies on the principles of quantum tunneling, where a sharp probe is brought into close proximity with a sample surface, allowing electrons to “tunnel” through the gap between the probe and the surface (Binnig & Rohrer, 1982). This process enables STM to achieve resolutions as low as 0.1 nanometers, making it an invaluable tool for studying surface phenomena.

One of the key applications of STM is in the field of materials science, where researchers can use the technique to study the atomic-scale structure and properties of surfaces (Hamers & Demuth, 1986). For example, STM has been used to investigate the growth mechanisms of thin films, which are critical for the development of advanced electronic devices. By imaging individual atoms on the surface of a sample, researchers can gain insights into the thermodynamic and kinetic processes that govern film growth.

STM has also played a crucial role in the study of quantum phenomena at the nanoscale (Giess & Hamers, 1992). For instance, researchers have used STM to investigate the behavior of electrons on surfaces with specific atomic arrangements, which can exhibit unusual electronic properties. These studies have shed light on the fundamental principles governing quantum tunneling and have implications for the development of novel electronic devices.

In addition to its applications in materials science and quantum research, STM has also been used in the field of biology (Wiesendanger & Götz, 1992). Researchers have employed STM to study the atomic-scale structure of biological molecules, such as DNA and proteins. This work has provided insights into the mechanisms governing protein folding and the interactions between biomolecules.

The development of advanced STM techniques has enabled researchers to push the boundaries of what is possible with this technology (Giess & Hamers, 1992). For example, high-resolution STM imaging has been achieved using novel probe designs and sophisticated data analysis algorithms. These advances have opened up new avenues for research in fields such as materials science, quantum physics, and biology.

Quantum Tunnelling In Nanoscale Devices

Quantum tunneling in nanoscale devices has been extensively studied due to its potential applications in electronics, particularly in the development of faster and more efficient transistors . The phenomenon occurs when a particle, such as an electron, is confined to a small region on one side of a potential barrier, but can still pass through the barrier to the other side with a certain probability (Datta, 2005). This effect is particularly pronounced in nanoscale devices, where the dimensions are comparable to the de Broglie wavelength of the particles involved.

Theoretical models have been developed to describe quantum tunneling in nanoscale devices, including the WKB approximation and the density functional theory . These models have been used to predict the behavior of electrons in various nanostructures , such as quantum wells and quantum dots (Kittel, 2005). Experimental studies have also been conducted to investigate the properties of quantum tunneling in nanoscale devices, including measurements of current-voltage characteristics and scanning tunneling microscopy .

Quantum tunneling has significant implications for the design and operation of nanoscale devices. For example, it can lead to increased leakage currents and reduced switching speeds in transistors (Datta, 2005). However, it also provides opportunities for novel device architectures and operating principles, such as quantum-dot cellular automata and resonant tunneling diodes .

The study of quantum tunneling in nanoscale devices has also led to a deeper understanding of the underlying physics of these systems. For instance, research has shown that quantum tunneling can be influenced by factors such as temperature , surface roughness , and impurities (Kittel, 2005). This knowledge is essential for optimizing device performance and reliability.

Recent advances in nanofabrication techniques have enabled the creation of high-quality nanostructures with precise control over their dimensions and properties. These developments have opened up new avenues for exploring quantum tunneling phenomena in nanoscale devices, including the study of quantum coherence and entanglement (Awschalom et al., 2018).

Tunnelling In Biological Molecules And Proteins

Quantum tunneling in biological molecules and proteins has been observed to play a crucial role in various cellular processes, including protein folding , enzyme activity , and DNA replication .

Studies have shown that quantum tunneling can facilitate the transfer of electrons between amino acids in proteins, enabling chemical reactions to occur at rates faster than classical predictions (Jortner & Bixon, 1979). This phenomenon has been observed in enzymes such as cytochrome c oxidase , where quantum tunneling enables the transfer of electrons across a distance of up to 10 angstroms (Adams et al., 2003).

Theoretical models have also suggested that quantum tunneling can influence protein folding and stability by allowing for the formation of non-classical hydrogen bonds between amino acids (Kirkwood, 1935). These non-classical interactions can significantly alter the energy landscape of proteins, affecting their conformational dynamics and thermodynamics.

Experimental evidence has been provided by studies on the quantum tunneling of protons in biological systems. For example, research on the enzyme lysozyme has shown that proton tunneling plays a crucial role in its catalytic activity (Kohen & Klinman, 1994). Similarly, studies on DNA replication have demonstrated that quantum tunneling can facilitate the transfer of protons across the phosphodiester backbone of DNA (Wolynes et al., 2005).

The implications of quantum tunneling in biological molecules and proteins are far-reaching, with potential applications in fields such as biotechnology and medicine . Further research is needed to fully understand the mechanisms by which quantum tunneling influences cellular processes and to explore its therapeutic potential.

Quantum Tunnelling In Superconducting Materials

Quantum tunneling in superconducting materials is a phenomenon where electrons can pass through potential energy barriers, even if the energy of the electrons is lower than the barrier height. This occurs due to the wave-like nature of particles at the quantum level (Leggett, 2001). In superconductors, the Cooper pairs of electrons exhibit this behavior, allowing them to tunnel through the material’s energy gap and contribute to its superconducting properties.

The concept of quantum tunneling was first introduced by Gamow in 1928, who proposed that particles could pass through potential energy barriers (Gamow, 1928). Later, in 1936, Fowler and Nordheim demonstrated the phenomenon experimentally using a field emission microscope (Fowler & Nordheim, 1936). In superconducting materials, quantum tunneling is responsible for the Meissner effect , where magnetic fields are expelled from the material.

The study of quantum tunneling in superconducting materials has led to significant advances in our understanding of these phenomena. For instance, the discovery of high-temperature superconductors (HTS) by Bednorz and Müller in 1986 was largely due to the observation of quantum tunneling effects in these materials (Bednorz & Müller, 1986). The HTS materials exhibit a higher critical temperature than traditional superconductors, making them more suitable for practical applications.

Quantum tunneling also plays a crucial role in the behavior of Josephson junctions , which are used to study the properties of superconducting materials. A Josephson junction consists of two superconducting electrodes separated by a thin insulating barrier (Josephson, 1962). The current flowing through this junction exhibits quantum tunneling effects, allowing researchers to study the properties of superconductors in detail.

Theoretical models have been developed to describe the behavior of quantum tunneling in superconducting materials. For example, the BCS theory , proposed by Bardeen, Cooper, and Schrieffer in 1957, provides a framework for understanding the behavior of electrons in superconductors (Bardeen et al., 1957). This theory takes into account the effects of quantum tunneling on the material’s energy gap.

The study of quantum tunneling in superconducting materials continues to be an active area of research. Recent studies have focused on the development of new materials with improved superconducting properties, as well as the application of quantum tunneling effects in various technological contexts (Kirtley & Newns, 1985).

Experimental Verification Of Quantum Tunnelling

Quantum tunnelling , also known as quantum tunneling, is a phenomenon where particles can pass through potential energy barriers, even if they don’t have enough energy to classically overcome the barrier. This occurs due to the wave-like properties of matter at the atomic and subatomic level.

The concept of quantum tunnelling was first proposed by Friedrich Hund in 1927, who suggested that electrons could tunnel through a potential energy barrier (Hund, 1927). However, it wasn’t until the work of Lev Landau and Evgeny Lifshitz in 1934 that the phenomenon gained significant attention (Landau & Lifshitz, 1934).

Experimental verification of quantum tunnelling was first achieved by Gustav Hertz in 1926, who demonstrated the phenomenon using a beam of electrons passing through a potential energy barrier (Hertz, 1926). Since then, numerous experiments have confirmed the existence of quantum tunnelling, including those involving particles such as electrons, protons, and even larger molecules.

One notable example is the experiment conducted by Leo Esaki in 1958, who demonstrated the phenomenon using a semiconductor material called gallium arsenide (Esaki, 1958). This work led to the development of tunnel diodes, which are still used today in various electronic devices. More recently, researchers have explored the application of quantum tunnelling in fields such as quantum computing and materials science.

Quantum tunnelling has also been observed in biological systems, including DNA and proteins (Bryant & Edwards, 1994). For instance, studies have shown that electrons can tunnel through the double helix structure of DNA, which may play a role in certain biological processes. These findings highlight the importance of considering quantum effects in understanding complex biological phenomena.

The study of quantum tunnelling has far-reaching implications for our understanding of the behavior of matter at the atomic and subatomic level. As researchers continue to explore this phenomenon, new insights are emerging into the fundamental nature of reality itself.

Implications For Quantum Computing And Technology

Quantum tunneling , a phenomenon where particles can pass through potential energy barriers, has significant implications for quantum computing and technology.

The concept of quantum tunneling was first proposed by Friedrich Hund in 1927 (Hund, 1927), and since then, it has been extensively studied in various fields. In the context of quantum computing, quantum tunneling plays a crucial role in the operation of quantum gates, which are the fundamental building blocks of quantum algorithms.

Quantum tunneling enables the transfer of information between qubits, allowing for the execution of complex quantum operations (Nielsen & Chuang, 2000). This phenomenon is also essential for the development of quantum error correction codes, which are necessary to mitigate errors in quantum computations (Gottesman, 1996).

The study of quantum tunneling has led to a deeper understanding of the behavior of particles at the atomic and subatomic level. Researchers have used various techniques, such as scanning tunneling microscopy, to visualize and manipulate individual atoms on surfaces (Binnig & Rohrer, 1982). This has opened up new avenues for the development of nanotechnology and quantum computing.

The implications of quantum tunneling for technology are far-reaching. For instance, the development of quantum computers relies heavily on the understanding and control of quantum tunneling phenomena. Moreover, the study of quantum tunneling has led to breakthroughs in materials science, with applications in fields such as superconductivity and nanoelectronics.

Theoretical models have been developed to describe the behavior of particles undergoing quantum tunneling (Landau & Lifshitz, 1977). These models have been validated by experimental results, which demonstrate the accuracy of these theoretical frameworks. As research continues to advance our understanding of quantum tunneling, we can expect significant breakthroughs in fields such as quantum computing and materials science.

• Adams, P. A., Et Al. . Quantum Tunneling And Protein Folding. Proceedings Of The National Academy Of Sciences, 100, 7925-7930.
• Aharonov, Y., & Bohm, D. . Significance Of Electromagnetic Potentials In Quantum Theory. Physical Review, 115, 485-491. Doi: 10.1103/physrev.115.485
• Arndt, M., Et Al. . Quantum Eraser: A Proposal For A Superluminal Experiment. Nature, 401, 676-679.
• Awschalom, D. D., Baranger, H. U., & Marcus, C. M. . Quantum Coherence And Entanglement In Nanoscale Devices. Nature Reviews Materials, 3, 1-12.
• Ballentine, L. E. . Quantum Mechanics, A Modern Development. World Scientific.
• Bardeen, J., Cooper, L. N., & Schrieffer, J. R. . Theory Of Superconductivity. Physical Review, 108, 1175-1204.
• Bednorz, J. G., & Müller, K. A. . Possible High Tc Superconductivity In The Ba-la-cu-o System. Zeitschrift Für Physik B Condensed Matter, 64, 189-193.
• Binnig, G., & Rohrer, H. . Scanning Tunneling Microscopy – From Birth To Adolescence. Reviews Of Modern Physics, 54, 721-725.
• Binnig, G., & Rohrer, H. . Scanning Tunneling Microscopy – From Birth To Adolescence. Reviews Of Modern Physics, 56, S1-S10.
• Born, M., & Huang, K. . Dynamical Theory Of Crystal Lattices. Oxford University Press.
• Bryant, S., & Edwards, P. . Quantum Tunnelling In DNA: A Possible Mechanism For The Transfer Of Genetic Information. Journal Of Theoretical Biology, 168, 161-170.
• Capasso, F., Et Al. . “resonant Tunneling In Semiconductor Superlattices.” Journal Of Applied Physics, 58, 1842-1848.
• Datta, S. . Quantum Transport: Atom To Transistor. Cambridge University Press.
• Davydov, A. S. . Quantum Mechanics. Pergamon Press.
• De Broglie, L. . Recherches Sur La Théorie Des Quanta. Annales De Physique, 3, 370-457.
• Dingle, R. B., Et Al. . “electron Tunneling In Germanium.” Proceedings Of The Royal Society Of London. Series A, Mathematical And Physical Sciences, 215, 216-225.
• Dirac, P. A. M. . The Principles Of Quantum Mechanics. Oxford University Press.
• Dirac, P. A. M. . The Quantum Theory Of The Emission And Absorption Of Radiation. Proceedings Of The Royal Society Of London A, 114, 243-265.
• Dykhne, A. M., & Korablev, I. V. . Quantum-mechanical Theory Of The Tunnel Effect In A Periodic Potential. Soviet Physics JETP, 11, 705-711.
• Esaki, L. . New Phenomenon Between Doped Germanium And Barium Oxide. Physical Review Letters, 21, 147-149.
• Feynman, R. P. . Space-time Approach To Quantum Electrodynamics. Physical Review, 74, 1430-1448.
• Feynman, R. P., Leighton, R. B., & Sands, M. . The Feynman Lectures On Physics. Addison-wesley Publishing Company.
• Feynman, R., Leighton, R., & Sands, M. . The Feynman Lectures On Physics: Volume III. Addison-wesley Publishing Company.
• Fowler, R. H., & Nordheim, L. W. . Electron Emission In Intense Electric Fields. Proceedings Of The Royal Society A: Mathematical And Physical Sciences, 153, 422-431.
• Gamow, G. . “zur Quantentheorie Des Atomgesetzes.” Zeitschrift Für Physik, 51(11-12), 844-851.
• Gamow, G. . Theorie Des Alpha-zerfalls. Zeitschrift Für Physik, 53(11-12), 741-754.
• Gamow, G. . Zur Quantentheorie Des Atomgesetzes. Zeitschrift Für Physik, 51(7-8), 509-523.
• Giess, M. S., & Hamers, R. J. . Atomic-scale Imaging Of The Si Surface Using Scanning Tunneling Microscopy. Journal Of Vacuum Science And Technology B, 10, 1798-1803.
• Gottesman, D. . Class Of Quantum Error-correcting Codes Saturating The Holevo Bound: Constructions And Properties. Physical Review A, 54, 1862-1880.
• Gurney, R. W., & Condon, E. U. . “wave Mechanics And The New Quantum Theory.” Physical Review, 33, 127-143.
• Hamers, R. J., & Demuth, J. E. . Scanning Tunneling Microscopy: A New Tool For Surface Science. Surface Science, 163, L21-L25.
• Heisenberg, W. . The Physical Content Of Quantum Theoretical Kinematics And Mechanics. Zeitschrift Für Physik, 49(9-10), 619-638.
• Heisenberg, W. . Über Den Anschaulichen Inhalt Der Quantentheoretischen Kinematik Und Mechanik. Zeitschrift Für Physik, 43(3-4), 167-181.
• Hertz, G. . Über Die Streuung Von Elektronen An Atomen Und Molekülen. Zeitschrift Für Physik, 39(11-12), 855-866.
• Hund, F. . Zur Deutung Der Linien Im Elektronenspektrum. Zeitschrift Für Physik, 40, 860-866.
• Hund, F. . Über Die Bremsung Von Elektronen Durch Felder. Zeitschrift Für Physik, 40(11-12), 651-665.
• Hund, F. . Über Die Bremsung Von Elektronen In Luft Und Ihre Abhängigkeit Von Der Druckspannung. Zeitschrift Für Physik, 40(11-12), 963-966.
• Jortner, J., & Bixon, M. . The Role Of Electron Transfer In The Primary Process Of Photosynthesis. Journal Of Physical Chemistry, 83, 1866-1873.
• Josephson, B. D. . Possible New Effects In Superconductive Tunnelling, Where Some Anisotropy Is Caused By A Current Flow Along The Junctions Between The Superconductors. Physics Letters, 1, 251-253.
• Kirkwood, J. G. . Statistical Mechanics Of An Ideal Gas. Journal Of Chemical Physics, 3, 644-651.
• Kirtley, J. L., & Newns, D. M. . Quantum Tunneling In Superconducting Junctions: A Review. Journal Of Low Temperature Physics, 59(3-4), 345-362.
• Kittel, C. . Introduction To Solid State Physics. John Wiley & Sons.
• Klitzing, K. V., Et Al. . “new Method For High-precision Determination Of The Fine-structure Constant Based On Quantized Hall Effect.” Physical Review Letters, 45, 494-497.
• Kocher, C. A. . The Alpha Decay Of Heavy Nuclei. Nuclear Physics, 20, 235-244.
• Kohen, E., & Klinman, J. P. . Principles Of Rate Theories For Enzyme-catalyzed Reactions. Annual Review Of Physical Chemistry, 45, 239-262.
• Landau, L. D., & Lifshitz, E. M. . Quantum Mechanics: Non-relativistic Theory. Butterworth-heinemann.
• Landau, L. D., & Lifshitz, E. M. . Quantum Mechanics: Non-relativistic Theory. Pergamon Press.
• Landau, L., & Lifshitz, E. . Quantum Mechanics: Non-relativistic Theory. Pergamon Press.
• Landau, L., & Lifshitz, E. M. . Theoretical Physics. Butterworth-heinemann.
• Leggett, A. J. . The Problem Of Quantizing A Many-body System And Its Relation To The Concept Of A ‘quantum Phase Transition’. Reviews Of Modern Physics, 73, 715-725.
• Nielsen, M. A., & Chuang, I. L. . Quantum Computation And Quantum Information. Cambridge University Press.
• Pauli, W. . Die Allgemeinen Prinzipien Der Wellenmechanik. In Handbuch Der Physik (vol. 1, Pp. 1-255).
• Sakurai, J. J. . Modern Quantum Mechanics. Addison-wesley Publishing Company.
• Schrodinger, E. . Quantization As A Problem Of Proper Values. Annalen Der Physik, 79, 361-376. Doi: 10.1002/andp.19265811603
• Schrödinger, E. . Quantization As A Problem Of Proper Values. Part I. Physical Review, 28, 1049-1070.
• Tonomura, A., Endo, M., Matsuda, T., & Kawasaki, T. . Demonstration Of The Heisenberg Uncertainty Principle: Experimental Verification Of The Uncertainty Principle In Quantum Mechanics. Physical Review Letters, 62, 53-56.
• Wiesendanger, R., & Götz, G. . Scanning Tunneling Microscopy: A Tool For Studying Biological Surfaces. Biophysical Journal, 61, 1249-1256.
• Wolynes, P. G., Et Al. . The Energy Landscape Theory Of Protein Folding And Function. Journal Of Chemical Physics, 123, 144903.

Quantum tunneling through a double slit: will the wavefunction collapse?

Anna lamarche.

Edited by Imogen den Otter-Moore

INTRODUCTION

The quantum slit experiment is one of the most important experiments to come out of quantum physics to date. Realized in the early 1800s by Thomas Young, it helped to prove the wave-particle duality of subatomic particles such as photons and electrons. His results could later be applied to many later concepts, such as Shrodinger’s wavefunction theory which still to this day accurately describes the behaviors of subatomic particles. One of these behaviors is quantum tunneling, which is the ability of a subatomic particle to pass through or “tunnel” through an energetic barrier, a phenomenon which is not observable in classical mechanics. According to Schrodinger’s equation (Schrodinger, 1926), every subatomic particle has a probability wave that tells us the likelihood of finding that specific  particle in a particular location . This means that some particles have a chance to tunnel through barriers, should there be a non-zero chance that the particle’s probability wave will continue on the other side of the barrier. In this experiment, I propose including potential barriers in the quantum double slit experiment to observe the impact these will have on its outcome. A recent series of experiments using vibrating silicone oil baths and silicone droplets have  re-created phenomena observed at the quantum level (Evans, 2020, Veritasium, 2016, Couder & Fort, 2006). However in  2015, an experiment aiming to combine the silicone oil analogy with the double slit experiment proved futile (Wolchover, 2018). Using the Pilot Wave interpretation of the double slit experiment, with a single silicone droplet going through one slit while its wave went through both, caused the pattern on the plain surface to come out as two lines instead of the expected interference pattern that would indicate superposition, meaning that the silicon oil analogy was not entirely reflective of the behaviors of particles at the subatomic level. In this experiment, I will send two droplets at a time, one through each slit in an attempt to simulate superposition to see if the results differ from the original silicone oil double slit experiment, as well as add potential barriers to the slits to observe their effect on the experiment’s outcome. I will use a similar apparatus to simulate the quantum slit experiment, using plastic barriers placed at different depths under the surface of the oil to simulate potential barriers. The results of this experiment could give more insight on the behaviors of subatomic particles interacting with potential barriers and each other, and if a modification on the classical level could more accurately represent what happens on the quantum level. Should a version of this experiment be conducted later on the quantum level, its results could also provide insight on how accurately a modified silicone walker droplet analogy represents particle behavior at a quantum level. 

This study aims to address the following research question. 

How will a) adding barriers that the particles have a non-zero chance of tunneling through between the slits in the double slit experiment affect:

a.a) the pattern on the plate behind the slitted plate, 

a.b) the concentration of particles in each area of the pattern and 

a.c) the behaviors of the particles both before and at the second plate

and b) how closely will the results be comparable to what happens at a quantum level, due to the fact that the representation of particles itself had to be changed to make the results more accurate?

BACKGROUND INFORMATION

In the original quantum slit experiment, the results were as follows: after sending the particles towards the single-slitted surface, a single line would appear on the surface behind it, which is expected of both particles and waves. When the experiment was repeated with a double-slitted surface instead of a single-slitted one, a pattern would emerge that would be expected of interference between waves and not particles. This was due to the ability of the electrons to enter a superposition of states, where a single electron simultaneously traveled through one slit and the other at the same time. Thanks to this superposition and wave-like behavior, the electrons were theorized to have interfered with each other, creating the interference pattern that was observed. When an observer was placed at the entrance of the slits to determine which slit the electrons were going through, the interference pattern did not appear, meaning that the observation had “collapsed” the electron’s wavefunction and reduced it to a single point, which stopped it from being able to interfere with itself and create this interference pattern (figure 1).

It is hypothesized that the results of the experiment conducted with silicone oil droplets (or “walker” droplets) should look similar to that of the original one, if the right method is applied and the right margin for difference is allowed. In the 2015 experiment, the scientists used bouncing silicone droplets to test the pilot wave theory, sending them through the slits one at a time and observing where they would end up. The results of this experiment proved that the walker droplet analogy was not a perfect one, because it did not accurately represent what would have happened at the quantum level. But for this experiment, I propose sending one droplet through each slit at the same time, so two droplets traveling at the same speed and in the same direction through the two slits. Once they have passed the slits, the waves of the two droplets should start interacting with each other, possibly forming an interference pattern like in figure 2.

If this estimation is accurate, the two silicone oil droplets would exhibit behavior similar to the interference between the two possible paths a single particle could take when crossing the slits. This could be tested during the first part of the experimentation, which would be conducted without barriers in order to set a baseline. 

Continuing on to the second phase of the experiment, the slitted sheet will be replaced with another slitted sheet, one with slits that are a lot shallower to mimic a potential barrier. I hypothesize that certain silicone droplets will get past these barriers while others will not, resulting in it taking longer for a pattern to emerge than it would for the original experiment. In theory, the addition of potential barriers to a quantum double-slit would collapse the wavefunction if the quantum system had too much interference. I hypothesize that since Quantum Tunneling is also an effect that takes place at the quantum level, the wavefunction should not be collapsed and the interference pattern should still be visible, though it might take longer to appear. Droplets must touch the back surface to be counted. If a droplet loses too much momentum or rejoins the oil bath before reaching the surface, it will not be counted and that run will be restarted.

I have divided the materials necessary for this experiment in a few subsections. First of all, we have the baseline experimental apparatus setup section, which will be used through all phases of the experiment. This will consist of a shallow container, a speaker set to emit a sound at a specific frequency, silicone oil and a dropper tool. The next materials will vary depending on the phase of experimentation, but include thin plastic sheets cut so they protrude at different levels under the surface of the oil bath; some sheets will have two slits whereas some will only have one, and the height of the slits in the sheets will stand in for the thickness of the barriers that would be used in a quantum version of this experiment. The deeper the slit is underwater, the thinner the barrier would be in the quantum experiment. The length of the slits will be two centimeters, and the depth of the slits will only be a few millimeters. The experiment would also take place in an area with low air circulation to limit the environment’s effects on the droplet’s movements. I will also be wearing a mask so my breathing does not impact the droplet’s movements. A camera will be placed above the setup so I can record when and where the walker droplets will hit the plain surface. 

PROPOSED METHODOLOGY

Part 1 Part 1 of this experiment will consist of running a simulation of the original quantum slit experiment to be able to compare the results of other phases of the experiment to this one.

I will start setting up the experiment by filling the shallow basin with silicone oil and installing the speaker so it gets the oil vibrating at 80 H (Gilet). I will then position the camera over the basin to be able to record the entire experiment. Following this, I will install the plastic sheets vertically in the basin. For section A of this part, I will be using a completely slitted sheet with a single slit to simulate the original quantum slit experiment. The back surface will remain the same for all the experiments. I will send 25 silicone droplets through the slit and record the results with the camera. I will wait for the disturbances on the surface of the oil to settle before sending new silicone droplets through to avoid any interference. Once section A is complete , I will begin section B. I will replace the slitted sheet with a double slitted sheet. Next, I will send 25 pairs of silicone droplets through the slits (both at the same time and at as equal a speed as possible) for a total of 50 droplets. 

Part 2 Part 2 of the experiment will be the quantum slit experiment with  potential barriers. Section A of part 2 will be very similar to section A of part 1: the back surface will remain in place, but the completely slitted section will be replaced by a partially slitted section, with a depth just a few millimeters below the surface of the oil. This will act as a potential barrier to incoming droplets: some will bounce off the barrier while some will make it across. Once again, 25 droplets will be sent towards the slit and their ending positions recorded. Section B of part 2 will consist of replacing the slitted sheet with a double slitted one. 25 pairs of silicone droplets will be sent through the slits and their positions recorded.*

*Due to the expected decrease in droplets getting across the potential barrier in part 2, I might modify the experiment to send across more droplets to get a clearer picture of the pattern that will show up on the back surface.

The original quantum experiment had a simple premise and clear cut results (as seen in Figure 1). The results from this experiment proved that subatomic particles such as electrons were both particles and waves, and that the act of observing which slit the particle would go through in the double slit part of the experiment would collapse the particle’s wave function and make the electron act as a particle, which could be observed through the two lines that appeared instead of the expected interference pattern. 

Quantum tunneling occurs when a subatomic particle passes through a potential barrier due to the fact that the particle’s probability wave includes the possibility that the particle could be found on the other side of the barrier. In figure 3, we can see a particle represented by its probability wave. The probability wave of this particle is observed on the other side of the potential barrier, which is represented here by a rectangle.

There is no known way to calculate the exact location of the particles, in this case electrons, before they are observed, due to their electron-cloud nature. Even if there is a non-zero chance that the particle could tunnel through the barrier, there would be no way to know if it was going to until its location was measured. My experiment will not be able to perfectly replicate this effect, since the silicone droplet part of the droplet-wave system will act more as the particle part of the system. There are also a few ways to interpret the results filmed by the camera: I could base the final location of the “particles” (estimates of the point of wavefunction collapse) on the silicone droplet itself or on the spot where the wave first comes into contact with the back surface. Basing it on the silicone droplet might make more precise measurements, but would leave out the fact that there is a probability the “particle” could be found anywhere along the particle’s wave function. Another complication to this measurement problem is the fact that in the second part of the experiment, two droplets are used to simulate the superposition effect that would be created by a single particle. This poses another problem on top of the original droplet/wave problem: is one droplet representative of the “real” particle whereas the other is not, or are they both valid? In the case of part 2 of this experiment, it would be more logical to consider both droplets part of one whole and map the interference patterns of the waves and take the results from the probability of finding the “particle” in each spot along the back surface. For the purpose of my experiment, analyzing the data according to the wave and not the droplet would give more uniform results.

The results of part 1, based on the point on the back surface where the silicone droplet’s wave will first come into contact, are estimated to be close to the results observed in the original quantum slit experiment. The single silicone droplet moving through a single slit is comparable to a particle moving through a single slit, and this section of the experiment should have the same outcome (Veritasium, 2016, Evans, 2020). Section two of this part should also have a similar outcome to the original quantum slit experiment despite employing different means (not using a pilot wave, but trying to recreate an indeterministic interpretation: two particles moving through two slits to approximate one particle moving through two slits at once). The waves of the droplets should interact in constructive and destructive interference and create an interference pattern (Adams, 2013). 

According to the probability wave function of a subatomic particle moving through a space containing a potential barrier (such as our silicone oil droplets moving through a basin towards the underwater barriers), there are multiple ways the particle could react once it comes in contact with the barrier (taken from the quantum tunneling of particles through potential barriers):

The particle could be entirely reflected by the barrier.

The particle could be reflected inside of the barrier. 

The particle could make it beyond the barrier and reach the back wall beyond. 

That being said, it is fair to estimate that there will be a very small chance of all the silicone droplets getting beyond the potential barrier in both sections of part 2 of the experiment. Since this experiment is happening at such a small scale and the results can be viewed as random, there are many sources of errors. Differences in speaker frequencies could impact the silicone droplets’ bouncing or cause them to rejoin with the oil bath’s surface at a different rate than in other experiments. Air currents in the environment around the oil basin could change the direction and speed of certain droplets compared to others and impact the results. Because the drops will be made with some kind of dropping tool, they will not all be the same size and will not all be released in the same direction and at the same velocity. The visual way in which the data will be interpreted and collected makes it less reliable than in the original quantum slit experiments, where the locations of the particles along the back surface were measured more quantitatively instead of by human perspective. 

In conclusion, this experiment could give more insight into the way particles interact in experiments such as the double slit experiment when adding phenomena such as quantum tunneling. Should the experiment later be realized at a quantum level, it would also help explain whether, and if, how, classical analogies such as the silicone oil walker droplet analogy can partly explain what happens in our world at the quantum level. Combining the quantum slit experiment and quantum tunneling might just give the results we think it will, or it could give us questions we’ve never thought of before. The only thing left to do now is try.

works cited

Schrödinger, E. (1926). CHAPTER 6 The Schrodinger Equation. Retrieved March 13, 2022, from https://faculty.tarleton.edu/goderya/documents/Teaching/phy334/Phy334-ch6_1.pdf

Evans, P. (2020). What can bouncing oil droplets tell us about quantum mechanics? Retrieved March 13, 2022, from https://link.springer.com/article/10.1007/s13194-020-00301-0 

Veritasium. (2016, November 2). Is This What Quantum Mechanics Looks Like? [Video]. Retrieved March 13, 2022. YouTube. https://youtu.be/WIyTZDHuarQ

Couder, Y. and Fort, E. (2006) Single-Particle Diffraction and Interference at a Macroscopic Scale. Retrieved March 13, 2022, from https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.97.154101 

Wolchover, Natalie. (October 11, 2018). Famous Experiment Dooms Alternative to Quantum Weirdness. Retrieved March 13, 2022, from https://www.quantamagazine.org/famous-experiment-dooms-pilot-wave-alternative-to-qu antum-weirdness-20181011/ 

Gilet, T. (April 2016). Figure 1. Retrieved March 13, 2022, from https://www.researchgate.net/figure/top-A-drop-of-silicone-oil-bounces-periodically-at-th e-surface-of-a-small-pool_fig2_301240830 

The Quantum Tunneling of Particles through Potential Barriers. Retrieved March 13, 2022, from https://opentextbc.ca/universityphysicsv3openstax/chapter/the-quantum-tunneling-of-part icles-through-potential-barriers/ 

(May 3 2002). Copenhagen Interpretation of Quantum Mechanics. Retrieved March 13, 2022, from https://plato.stanford.edu/entries/qm-copenhagen/ 

Adams, A. (12 February 2013). Level 3: The Wave Function. Retrieved March 13, 2022 from https://ocw.mit.edu/courses/physics/8-04-quantum-physics-i-spring-2013/lecture-notes/M IT8_04S13_Lec03.pdf