millikan oil drop experiment class 12

Class 12 Physics Electrons Notes

Unit – 5  Modern Physics Chapter – 20 Electrons

• Class 12 Physics Notes
• Class 12 Notes
• Class 12  Practical File
• Class 12  Question Papers 
• Class 12 Important Questions

The sub-atomic particle with a negative charge of about 1.6 x 10ˆ-19 C and having 9.1 x 10ˆ-31 kg is known as an electron.

Millikan’s oil drop Experiment

Millikan determines the value of the charge of an electron using an experiment known as Millikan’s oil drop experiment.

Millikan’s oil drop experiment is based on stoke’s law of viscosity. This law state, “When the sphere of radius ‘r’ falling through a viscous medium of co-efficient of viscosity (ղ) under the action of many forces. It attains steady velocity is called terminal velocity and force on Sphere ‘s’.

Construction 

Fig: Millikan’s oil drop Experiment

The experimental arrangement of this experiment Consists of the double-walled chamber having two windows W₁ and W₂ as shown in the fig above. The window W₁ is used to pass light in order to illuminate (shine). The oil drop and window ‘ W₂’ is used to pass x-ray In order to ionize the oil drop inside the double-walled chamber, there are two metal plate A & B where Plate A have a hole at its center. The upper plate (A) is connected to a high-tension battery while the lower plate is connected to the ground. Lock oil (a non-volatile liquid ) can be sprayed into the hole at Upper Plate ‘A’ with the help of an atomizer. The microscope Is provided with a crosswire and micrometer scale. So that the motion of the oil drop can be observed and measured.

1. Motion of oil drop under gravity.

When an electric field is not applied, the oil drop fans under gravity with increasing velocity. when the viscous force act on oil drop, then its velocity becomes Constant called terminal velocity.

r =radius of oil drop

ৎ =density of oil drop

σ = density of air

V₁ = terminal velocity

F = viscus force

U = Upthrust

Wight of oil drop (W1) = mass of oil drop x g

Again, 

Upthrust due to air (u) = weight of air displaced by oil drop 

Also, 

Viscus force (F) = σπηrV

When oil drops move with constant velocity,

equation (i) measures the radius of oil drop.

2. The motion of oil drop under electric field

When a strong field is applied between two plates, the negatively charged oil drops move in an upward direction and soon attain a terminal velocity (V2) in an upward direction. 

Also let ‘E’ be electric field intensity and ‘q’ be the charge, the electric force on oil drop in an upward direction be

fe = q.E 

Viscus force in a downward direction is 

When the oil drop attains terminal velocity V2 then,

equation(ii) gives the charge of oil drop

3. When oil drop is at rest or stationary

q = ne   [∴ where n =no. of electron  ,e = charge of electron]

 where ,

v = Potential difference

d =  Separations between two plates

v = volume of oil drop

r = radius of oil drop

p = density of oil

 Deflection of the electron inside the electric field

Let us consider an electron of charge ‘e’ is inside the electric field of strength ‘E’ as shown in the figure. Then force experiment by an electron inside the electric field,

Thus, The acceleration produced on this electron is, 

where m = mass of the electron.

If ‘y’ is the deflection in the vertical direction in time ‘t’, then;

If ‘x’ be the horizontal distance in time, ‘t’,

using equation (iii) in (ii),

If ‘V’ be the p.d between two plates of separation ‘d’ then the electric field is given by; 

Then, equation (iv) becomes; 

Equation (v) represent the equation of parabola hence the path of an electron field is parabolic in nature. 

When the electron just passes the plate x = D then equation (A) becomes.

Let, θ be the angle at which the beam emerged out from the field then,

The motion of electrons in a magnetic field

Let us consider a beam of an electron moving with velocity ‘v’ horizontally entering inside uniform magnetic Field ‘B’ perpendicular to the direction of ‘V’ when it enters inside the magnetic field, a Lorentz force act on an electron beam which is given by

This force is perpendicular to both B and V. Due to this electron is deflected into a circular path as shown in the figure above

Let ‘m’ be the mass of the electron and ‘r’ be the radius of the circular path inside the magnetics field. Then,

Lorentz force provides the necessary centripetal force

This relation gives the radius of the circular path Also,

So, the frequency of electron inside the magnetic field is given by,

And, Time period of an electron inside a magnetic field is,

Where, 

E = V/d, Electric field intensity 

B = Magnetic field 

v = velocity, V = P.d. 

e = charge 

M = mass of electron

J.J Thomson Experiment

J.J Thomson discusses an experiment to determine the specific charge (e/m) of an electron which is known as J.J Thompson’s experiment.

When a beam of the electron is subjected to the uniform electric field and magnetic field acting perpendicular to each other in such a way that deflection is produced by another. Then the path of a beam of the electron remains undeflected.

Construction

 Fig: Experimental Arrangement of J.J Thomson Experiment

The experimental arrangement of J.J Thomson consists of cathode [c] and anode [A] which are enclosed in an evacuated discharge tube. When high voltage is applied between cathode and anode a fine beam of electrons emits from the cathode and through the hole of the anode they pass between two parallel plates p1 and p2

When an electric field is applied between two plates p1 and p2 then electron beams are deflected upward and appear at position ‘s1’. And when the magnetic field is applied the electron beam is deflected downward and appears at position ‘s2’. But, when both an electric field and a magnetic field are applied, then electron beams remain un-deflected and appear at position ‘s’.

 Theory 

When a potential difference (vo) is applied between cathode and anode, the beam of the electron is highly accelerated and gains a velocity ‘v’, whose K.E is given by ;

When both magnetic field and electric field are applied perpendicular to each other such that the beam of the electron does not bend. Then, the magnetic field force and electric force are equal;

i.e Magnetic force = Electric field 

Using equation (ii) in equation (i); 

If ‘V’ be the potential difference between two plates and ‘d’ be the separation between them.

using equation (iv) in (iii);

By knowing the value of V, B, d, and vo, we can find the value of e/m or a specific charge

By using J.J Thomson’s experiment and Millikan’s oil drop experiment we can calculate, 

If you want to ask anything, please contact us by Messaging us on Social Media.     Social Media links:-

Class 12 Physics Notes 2078: Complete Physics Guide (New Syllabus) | Questions Answers and Guide | Class 12 Physics Book Solution Guide  | Class 12 Physics Book PDF 2078 Solution | Class 12 Physics Book Notes 2078 Guide | Class 12 Physics All Chapter Notes | Physics Chapter Wise Notes. Class 12 Physics Electrons Notes.

Sir,could you please send the guide of physics,chemistry,biology in the form of pdf in this website?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Talk to our experts

1800-120-456-456

• Millikan's Oil Drop Experiment

Introduction

The oil drop experiment was performed in 1909 by Robert A. Millikan and Harvey Fletcher to measure the elementary electric charge (it means the electron's charge). This experiment took place in the Ryerson Physical Laboratory, which is present at the University of Chicago. Also, this experiment has proved to be very crucial in physics.

Before this experiment, the existence of subatomic particles was not accepted universally. Millikan's apparatus has an electric field created between a parallel pair of metal plates held apart by an insulating material. The oil droplets, which are electrically charged, enter the electrical field and are balanced between two plates by altering the field. When the charged drops fell at a constant rate, the gravitational forces and electric forces on it were equal.

Principles of Millikan's Experiment

The Millikan experiment is complicated and fiddly while performing in school. It is more likely that we will use a simulation or a film clip of the experiment to show its principles to the students. Few of such principles are,

An oil drop can fall under its own weight. If a charge is given to the drop, it can be suspended by using an electric field. At this point, the electrostatic force balances the weight of every drop. Then the size of the electrostatic force depends entirely on the drop. So Millikan should have figured out the charge as soon as he knew the weight.

Millikan allowed the drop to fall through the air to find the weight of the drop. It reaches its terminal velocity quickly. At this point, the weight is balanced by the viscous drag of the air. Drag can be calculated from the Stokes' Law, which allowed Millikan to determine the weight.

Millikan repeated the same experiment thoroughly for over 150 oil drops and selected 58 of Millikan oil drop experiment results and got to find the highest common factor. It means the single unit of charge that could be multiplied up to give the charge he measured on all of his oil drops.

Oil Drop Experiment

Millikan allowed charged small oil droplets to travel through a hole into an electric field in the experiment. With the electric field's varying strength, the charge over an oil droplet is calculated, and it always comes as a fundamental value of 'e.'

(Image will be uploaded soon)

Millikan and Fletcher designed the experiment apparatus. It included two metal plates held at a distance by an insulated rod. There were four holes in the plate, three of which were there to allow light to pass through, and one was there to allow viewing through the microscope.

They did not use ordinary oil for this experiment, as it would evaporate by the heat of the light, and could cause an error in the Millikan Oil Drop Experiment. The oil, which is usually used in a vacuum apparatus with low vapour pressure, was also used.

Oil passes through the atomizer, from where it came in tiny droplets form. The same droplets pass through the holes in the upper plate of the apparatus.

The droplet's downward movements are observed through the microscope and the mass of the oil droplets, and then their terminal velocity is measured.

The air present inside the chamber is ionised by passing through the X-ray beam. Collisions obtain the electrical charge on these oil droplets with gaseous ions produced by the ionisation of air.

Then, the electric field is set up between the two plates so that the motion of the charged oil droplets can be affected by the same electric field.

Now, gravity attracts the oil in a downward direction, and the electric field pushes the charge upwards. Also, the electric field strength is regulated so that all the oil droplets reach an equilibrium position with gravity.

The charge on the droplet is calculated at equilibrium, which depends on the mass of the droplet and strength of the electric field.

Millikan Oil Drop Experiment Calculations

The experiment initially allows the oil drops to fall between the plates in the absence of the electric field. They accelerate first due to gravity, but gradually the oil droplets slow down because of air resistance.

The Millikan oil drop experiment formula can be given as below.

F up = Q ⋅ E   F down = m

Where Q is an electron’s charge, m is the droplet’s mass, E is the electric field, and g is gravity.

Q ⋅ E = m ⋅ g

By this, one can identify how an electron charge is measured by Millikan. Millikan also found that all the drops had charges, which were 1.6x 10 -19 C multiples.

Importance of Millikan's Oil Drop Experiment

Millikan's experiment is quite essential because it establishes the charge on an electron.

Millikan used a simple apparatus in which he balanced the actions of electric, gravitational, and air drag forces.

Using the apparatus, he was able to calculate the charge on an electron as 1.60 × 10 -19 C.

The charge for any oil droplet is always an integral value of e (1.6 x 10 -19 ). Thus, Millikan's Oil Drop Experiment concludes that the charge is said to be quantized, which means that the charge on any particle will be an integral multiple of e always.

Millikan discovered the charge on a single electron using a uniform electric field between the oil drops and two parallel charged plates.

FAQs on Millikan's Oil Drop Experiment

1. What is Millikan’s Oil Drop experiment?

In 1909, Robert Millikan and Harvey Fletcher conducted the canvas drop trial to determine the charge of an electron. They suspended bitsy charged driblets of canvas between two essence electrodes by balancing downcast gravitational force with upward drag and electric forces. The viscosity of the canvas was known, so Millikan and Fletcher could determine the driblets’ millions from their observed diameters (since from the diameters they could calculate the volume and therefore, the mass). Using the known field and therefore the values of graveness and mass, Millikan and Fletcher determined the charge on canvas driblets in mechanical equilibrium. By repeating the trial, they verified that the charges were all multiples of some abecedarian value. They calculated this value to be1.5924 × 10 −19 Coulombs (C), which is within 1 of the presently accepted value of1.602176487 × 10 −19 C. They proposed that this was the charge of one electron.

2. How did the process work?

The outfit incorporated a brace of essence plates and a specific type of canvas. Millikan and Fletcher discovered it had been stylish to use a canvas with a particularly low vapor pressure, similar together designed to be used during a vacuum outfit. Ordinary canvas would dematerialize under the heat of the light source, causing the mass of the canvas to drop to change over the course of the trial.

By applying an implicit difference across a resemblant brace of vertical essence plates, an invariant electric field was created in the space between them. A ring of separating material was used to hold the plates piecemeal. Four holes were dug into the ring — three for illumination by a bright light and another to permit viewing through a microscope. A fine mist of canvas driblets was scattered into a chamber above the plates. The canvas drops came electrically charged through disunion with the snoot as they were scattered. Alternatively, the charge could be convinced by including an ionizing radiation source ( similar to an X-ray tube).

3. Describe the Millikan’s Oil Drop experiment procedure?

Canvas is passed through the atomizer from where it came in the form of bitsy driblets. They pass the driblets through the holes present in the upper plate of the outfit.

The downcast movements of driblets are observed through a microscope and the mass of canvas driblets also measure their terminal haste.

The air inside the chamber is ionised by passing a ray of X-rays through it. The electrical charge on these canvas driblets is acquired by collisions with gassy ions produced by the ionisation of air.

The electric field is set up between the two plates and so the stir of charged canvas driblets can be affected by the electric field.

Graveness attracts the canvas in a downcast direction and the electric field pushes the charge overhead. The strength of the electric field is regulated so that the canvas drop reaches an equilibrium position with graveness.

The charge over the drop is calculated at equilibrium, which depends on the strength of the electrical field and the mass of the drop.

4. Explain Millikan’s Oil Drop experiment in detail?

Millikan’s original trial or any modified interpretation, similar to the following, is called the canvas-drop trial. An unrestricted chamber with transparent sides is fitted with two resemblant essence plates, which acquire a positive or negative charge when an electric current is applied. At the launch of the trial, an atomizer sprays a fine mist of canvas driblets into the upper portion of the chamber. Under the influence of gravity and air resistance, some of the canvas driblets fall through a small hole cut in the top essence plate. When the space between the essence plates is ionized by radiation (e.g., X-rays), electrons from the air attach themselves to the falling canvas driblets, causing them to acquire a negative charge. 

A light source, set at right angles to a viewing microscope, illuminates the canvas driblets and makes them appear as bright stars while they fall. The mass of a single charged drop can be calculated by observing how presto it falls. By confirming the implicit difference, or voltage, between the essence plates, the speed of the drop’s stir can be increased or dropped; when the quantum of upward electric force equals the given downcast gravitational force, the charged drop remains stationary. The quantum of voltage demanded to suspend a drop is used along with its mass to determine the overall electric charge on the drop.

Through the repeated operation of this system, the values of the electric charge on individual canvas drops are always whole- number multiples of the smallest value — that value being the abecedarian electric charge itself (about1.602 × 10 −19 coulomb). From the time of Millikan’s original trial, this system offered satisfying evidence that electric charge exists in introductory natural units. All posterior distinct styles of measuring the introductory unit of electric charge point to its having the same abecedarian value. 

5. How does Millikan’s Oil Drop experiment work?

Simplified scheme of Millikan’s canvas-drop trial This outfit has a resemblant brace of vertical essence plates. An invariant electric field is created between them. The ring has three holes for illumination and one for viewing through a microscope. A specific type of canvas is scattered into the chamber, where drops come electrically charged. The driblets enter the space between the plates and can be controlled by changing the voltage across the plates. 

The driblets entered the space between the plates and, because they were charged, they could be controlled by changing the voltage across the plates. Originally, the canvas drops were allowed to fall between the plates with the electric field turned off. The snappily reached terminal haste due to disunion with the air in the chamber. The field was turned on and, if it was large enough, some of the drops (the charged bones) would start to rise. This is because the overhead electric force, FE, is lesser for them than the down gravitational force,g. (A charged rubber rod can pick up bits of paper in the same way.) A likely-looking drop was named and kept in the middle of the field of view by alternatively switching off the voltage until all the other drops fell. The trial was continued with this single drop. Millikan’s canvas drop trial measured the charge of an electron. Before this trial, the actuality of subatomic patches wasn't widely accepted. 

Millikan’s outfit contained an electric field created between a resemblant brace of essence plates, which were held piecemeal by separating material. Electrically charged canvas driblets entered the electric field and were balanced between two plates by altering the field. 

6. Why was the Negative Plate Earthed in Millikan's Oil Drop Experiment?

There are three possible reasonable ways to clear it.

The first reason is safety. Grounding ("earthing," in this context), the equipment is so important, particularly the time when you are working with high voltages. The same would be applied to protecting the equipment and for personal safety as well.

The second reason would be to establish a good stable reference point for the voltage measurement. A massive and solidly connected grounding cable would perform that job in a better way.

Finally, from an electrical standpoint, the two plates used in Millikan's experiment form a capacitor. On the other side, this capacitor is being charged to a very high voltage. In such cases, it is suggested to have a discharge path on one of the terminals or plates in order to avoid damage to either humans or equipment as well. Therefore, the negative plate is earthed.

7. Why do we Use Oil Instead of Other Liquids in the Millikan Oil-drop Experiment?

Oil is one of the best liquids for Millikan's oil drop experiment. It retains its mass over a while and exposes to higher temperatures. Also, we employ an atomizer for ultra-fine droplets. So less dense liquids like water and oils are preferred over water because water cannot survive at such higher temperatures.

The atomizer employment is also an important reason behind using oil for this experiment. Moreover, it should be noted that oil would retain the exact volume/mass/weight. This would enable an exact measurement of the charge. Other liquids would separate or dissipate or even evaporate.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.12: Oil Drop Experiment

• Last updated
• Save as PDF
• Page ID 52799

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

"How tall are you? How much do you weigh?" Questions like these are easy to answer because we have tools to make the measurements. A yard stick or tape measure will suffice to measure height. You can stand on a bathroom scale and determine your weight.

It is a very different matter to measure properties of objects that we cannot see with the naked eye. If we want to measure the size of a germ, we have to use a microscope. To learn the size of a single molecule, we have to use even more sophisticated instruments. So how would we measure something even smaller than a molecule, even smaller than an atom?

Charge and Mass of the Electron

The man who measured properties of the electron was Robert Millikan (1868-1953). He taught himself physics while a student at Oberlin College' since there was nobody on the faculty to instruct him in this field. Millikan completed postgraduate research training in the U.S. and in Germany. His studies on the properties of the electron proved to be of great value in many areas of physics and chemistry.

Oil Drop Experiment

Millikan carried out a series of experiments between 1908 and 1917 that allowed him to determine the charge of a single electron, famously known as the oil drop experiment. 

Millikan sprayed tiny drops of oil into a chamber. In his first experiment, he simply measured how fast the drops fell under the force of gravity. He could then calculate the mass of the individual drops. Then, he sprayed oil drops and applied an electrical charge to them by shining x-rays up through the bottom of the apparatus. The x-rays ionized the air, causing electrons to attach to the oil drops. The oil drops picked up static charge and were suspended between two charged plates. Millikan was able to observe the motion of the oil drops with a microscope and found that the drops lined up in a specific way between the plates, based on the number of electric charges they had acquired.

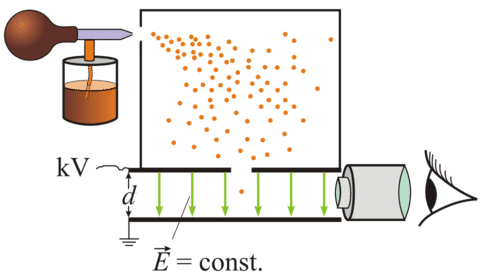
Millikan used the information to calculate the charge of an electron. He determined the charge to be \(1.5924 \times 10^{-19} \: \text{C}\), where \(\text{C}\) stands for coulomb , which is one ampere*second. Today, the accepted value of the charge of an electron is \(1.602176487 \times 10^{-19} \: \text{C}\). Millikan's experimental value proved very accurate; it is within \(1\%\) of the currently accepted value. Millikan later used the information from his oil drop experiment to calculate the mass of an electron. The accepted value today is \(9.10938215 \times 10^{-31} \: \text{kg}\). The incredibly small mass of the electron was found to be approximately 1/1840 the mass of a hydrogen atom. Therefore, Scientists realized that atoms must contain another particle that carries a positive charge and is far more massive than the electron.

• The oil drop experiment allowed Millikan to determine the charge on the electron.
• He later used this data to determine the mass of the electron.
• How did Millikan learn physics in college?
• What did Millikan use to pick up static charge?
• Where did the oil drops go to be measured?